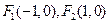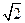题目内容
已知椭圆与双曲线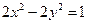
共焦点，且过（
）
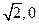（1）求椭圆的标准方程.
（2）求斜率为2的一组平行弦的中点轨迹方程；
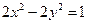共焦点，且过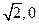（）（1）求椭圆的标准方程.
（2）求斜率为2的一组平行弦的中点轨迹方程；
（1）
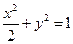
（2）y=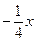
(
)
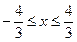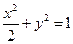
（2）y=
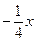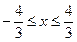()(1)依题意得，将双曲线方程标准化为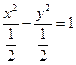
，则c=1
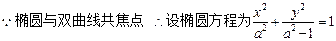
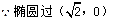
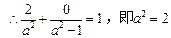
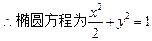
(2) 依题意，设斜率为2的弦所在直线的方程为y=2x+b，弦的中点坐标为（x，y），则
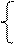y=2x+b
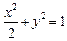得9x2+8xb+2b2—2="0 "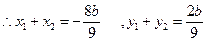 
即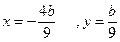
两式消掉b得y=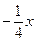
令△=0，64b2-36(2b2-2)=0，即b=±3，所以斜率为2，且与椭圆相切的直线方程为y=2x±3
即当x=
时斜率为2的直线与椭圆相切.
所以平行弦得中点轨迹方程为：y=()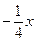
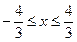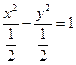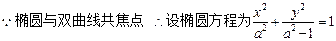
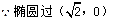
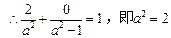
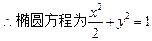
，则c=1(2) 依题意，设斜率为2的弦所在直线的方程为y=2x+b，弦的中点坐标为（x，y），则
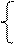y=2x+b 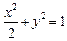得9x2+8xb+2b2—2="0 "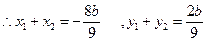 即
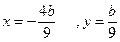两式消掉b得y=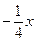令△=0，64b2-36(2b2-2)=0，即b=±3，所以斜率为2，且与椭圆相切的直线方程为y=2x±3
即当x=
时斜率为2的直线与椭圆相切.所以平行弦得中点轨迹方程为：y=
()
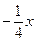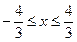练习册系列答案
相关题目
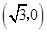，一条渐近线m:
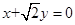，设过点A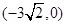
的直线l的方向向量
。
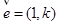，且a与l的距离为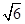
，求K的值；
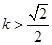时，在双曲线C的右支上不存在点Q，使之到直线l的距离为
⊥x轴于点C， 
，
,动点
到直线
交点
两点（
满足
,求直线
的斜率的取值范围
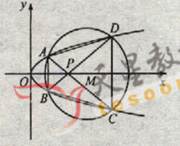(22) （本小题满分12分）（注意：在试题卷上作答无效）如图，已知抛物线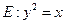
与圆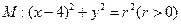
相交于A、B、C、D四个点。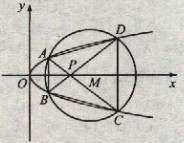
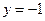的距离比它到点F
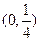的距离大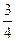
.
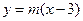对称，求实数
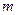的取值范围.
。
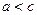