题目内容
【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1.
(1)求f(x)的解析式;
(2)若关于x的方程f(x)=x+m有区间(﹣1,2)上有唯一实数根,求实数的取值范围(注:相等的实数根算一个).
【答案】
(1)解:设f(x)=ax2+bx+c(a≠0),代入f(x+1)﹣f(x)=2x,
得2ax+a+b=2x,对于x∈R恒成立,故 ![]() ,又由f(0)=1,得c=1,
,又由f(0)=1,得c=1,
解得a=1,b=﹣1,c=1,∴f(x)=x2﹣x+1.
(2)解:由方程f(x)=x+m得x2﹣2x+1﹣m=0,令h(x)=x2﹣2x+1﹣m,x∈(﹣1,2),
即要求函数h(x)在(﹣1,2)上有唯一的零点,
①h(﹣1)=0,则m=4,代入原方程得x=﹣1或3,不符合题意;
②若h(2)=0,则m=1,代入原方程得x=0或2,满足题意,故m=1成立;
③若△=0,则m=0,代入原方程得x=1,满足题意,故m=0成立;
④若m≠4且m≠1且m≠0时,由 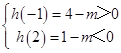 得1<m<4.
得1<m<4.
综上,实数m的取值范围是{0}∪[1,4).
【解析】(1)根据二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1,利用待定系数法,可得f(x)的解析式;(2)若关于x的方程f(x)=x+m有区间(﹣1,2)上有唯一实数根,则函数h(x)在(﹣1,2)上有唯一的零点,分类讨论,可得实数m的取值范围.
【考点精析】认真审题,首先需要了解函数的概念及其构成要素(函数三要素是定义域,对应法则和值域,而定义域和对应法则是起决定作用的要素,因为这二者确定后,值域也就相应得到确定,因此只有定义域和对应法则二者完全相同的函数才是同一函数),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案