Question

【题目】在直角坐标系中，已知射线OA：x﹣y=0（x≥0），OB：2x+y=0（x≥0）．过点P（1，0）作直线分别交射线OA，OB于点A，B．
（1）当AB的中点在直线x﹣2y=0上时，求直线AB的方程；
（2）当△AOB的面积取最小值时，求直线AB的方程．
（3）当PAPB取最小值时，求直线AB的方程．

Answer 1

【答案】
（1）解：设A（a，a），B（b，﹣2b），则线段AB的中点为C ．

∴ ﹣2× =0， = ，

分别化为：a=5b，a+2b﹣3ab=0．

解得： ，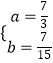

∴直线AB的方程为：y﹣0= （x﹣1），化为：7x﹣4y﹣7=0

（2）解：设A（a，a），B（b，﹣2b），（a，b＞0）．

a=b=1时，A（1，1），B（1，﹣2），S△OAB= ×|OP|×|AB|= = ．

a，b≠1时，S△OAB= ×|OP|×（a+2b）= （a+2b），

又 ，化为a+2b=3ab，

∴a+2b=3ab= ≤ ，解得：a+2b≥ ．

∴S△OAB≥ × = ，

当且仅当a=2b= 时取等号．

综上可得：当△AOB的面积取最小值 时，直线AB的方程为：y= （x﹣1），化为：4x﹣y﹣4=0

（3）解：设直线AB的方程为：my=x﹣1. ．

联立 ，解得A ，可得|PA|= = ．

联立 ，解得B ，可得|PB|= = ．

∴|PA||PB|= = = =f（m），

m=﹣3时，f（﹣3）=1；

令m+3=k≠0，f（m）=g（k）= = ，

k＜0时，g（k）= ≥ = ．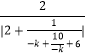

k＞0时，g（k）= ≥ = ，

而 ＞ ，

∴g（k）的最小值为： ．

当且仅当k= 时取等号．

∴m= ﹣3．

∴直线AB的方程为：（ ﹣3）y=x﹣1

【解析】（1）设A（a，a），B（b，﹣2b），则线段AB的中点为C ．可得 ﹣2× =0， = ，联立解出a，b，即可得出．（2）设A（a，a），B（b，﹣2b），（a，b＞0）．a=b=1时，A（1，1），B（1，﹣2），S△OAB= ×|OP|×|AB|．a，b≠1时，S△OAB= ×|OP|×（a+2b）= （a+2b），又 ，化为a+2b=3ab，利用基本不等式的性质可得a+2b的取值范围．（3）设直线AB的方程为：my=x﹣1. ．联立 ，解得A ，可得|PA|= ．同理可得|PB|= ．可得|PA||PB．
进而得出最小值．|