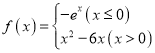题目内容
【题目】函数![]() 满足以下4个条件.
满足以下4个条件.
①函数![]() 的定义域是
的定义域是![]() ,且其图象是一条连续不断的曲线;
,且其图象是一条连续不断的曲线;
②函数![]() 在
在![]() 不是单调函数;
不是单调函数;
③函数![]() 是偶函数;
是偶函数;
④函数![]() 恰有2个零点.
恰有2个零点.
(1)写出函数![]() 的一个解析式;
的一个解析式;
(2)画出所写函数![]() 的解析式的简图;
的解析式的简图;
(3)证明![]() 满足结论③及④.
满足结论③及④.
【答案】(1)见解析 (2)见解析 (3)见解析
【解析】
(1)根据常见函数的性质写出满足条件的函数即可.
(2)根据常见函数的图像与函数的图像变换方法画图即可.
(3)根据函数![]() 满足定义域关于原点对称,且
满足定义域关于原点对称,且![]() 即可证明
即可证明![]() 为偶函数.直接求解函数的零点即可证明函数有两个零点.
为偶函数.直接求解函数的零点即可证明函数有两个零点.
本题为开放性题,答案不唯一,只需写出符合条件的函数即可,提供以下5个函数仅供参考.
(1)![]()
![]() (2)
(2) ![]()
![]()
(3)![]() (4)
(4)![]()
(5)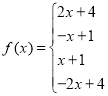
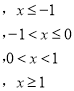
下面以函数![]() 为例给出证明:
为例给出证明:
证明:![]() 的定义域为R
的定义域为R
因为对定义域的每一个x,都有
![]()
所以函数![]() 是偶函数,
是偶函数,
又因为当![]() 时,
时,![]()
解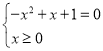 得
得![]()
所以当![]() 时,函数
时,函数![]() 只有一个零点,
只有一个零点,
又因为函数![]() 是偶函数,
是偶函数,
所以函数![]() 恰有2个零点.
恰有2个零点.

练习册系列答案
相关题目
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.