题目内容

【题目】已知是定义在上的奇函数，且满足，当时，，则函数在区间上所有零点的个数为（ ）

A.0B.2C.4D.6

【答案】D

【解析】

先讨论函数的性质，再根据函数性质画出草图；将零点的问题，转化为函数交点的问题，数形结合处理.

因为， 又函数是奇函数，故而是以4为周期的函数；

同时,故关于直线对称，

又=0的根个数，即方程的根的个数，

即函数与函数图像的交点的个数.

根据其在上的解析式，以及，画出两个函数的图像如图所示：

[Failed to download image : http://192.168.0.10:8086/QBM/2020/2/24/2405975385448448/2406501181480960/EXPLANATION/e0ab4516c45c47d9b69857d97722b5d5.png]

由图可知，两函数有5个交点，

故在区间的零点个数为6.

故选：D.

练习册系列答案
相关题目

【题目】在高一某班的元旦文艺晚会中，有这么一个游戏：一盒子内装有6张大小和形状完全相同的卡片，每张卡片上写有一个成语，它们分别为意气风发、风平浪静、心猿意马、信马由缰、气壮山河、信口开河，从盒内随机抽取2张卡片，若这2张卡片上的2个成语有相同的字就中奖，则该游戏的中奖率为________.

【题目】2017年10月18日至10月24日，中国共产党第十九次全国代表大会简称党的“十九大”在北京召开一段时间后，某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查，调查问卷共有20个问题，每个问题5分，调查结束后，发现这100名员工的成绩都在内，按成绩分成5组：第1组，第2组，第3组，第4组，第5组，绘制成如图所示的频率分布直方图，已知甲、乙、丙分别在第3，4，5组，现在用分层抽样的方法在第3，4，5组共选取6人对“十九大”精神作深入学习．

求这100人的平均得分同一组数据用该区间的中点值作代表；

求第3，4，5组分别选取的作深入学习的人数；

若甲、乙、丙都被选取对“十九大”精神作深入学习，之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度，求甲、乙、丙这3人至多有一人被选取的概率．

【题目】函数满足以下4个条件.

①函数的定义域是，且其图象是一条连续不断的曲线；

②函数在不是单调函数；

③函数是偶函数；

④函数恰有2个零点.

（1）写出函数的一个解析式；

（2）画出所写函数的解析式的简图；

（3）证明满足结论③及④.

【题目】已知函数的部分图象如图所示，分别是图象的最高点与相邻的最低点，且，，为坐标原点.

(1)求函数的解析式；

(2)将函数的图象向左平移1个单位后得到函数的图象，求函数的值域.

【题目】某手机企业为确定下一年度投入某种产品的研发费用，统计了近年投入的年研发费用千万元与年销售量千万件的数据，得到散点图1，对数据作出如下处理：令，，得到相关统计量的值如图2：

（1）利用散点图判断和哪一个更适合作为年研发费用和年销售量的回归类型（不必说明理由），并根据数据，求出与的回归方程；

（2）已知企业年利润千万元与的关系式为（其中为自然对数的底数），根据（1）的结果，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用？

【题目】已知函数（，）的图象的相邻两条对称轴之间的距离为4，且有一个零点为.

（1）求函数的解析式；

（2）若，且，求的值；

（3）若在上恒成立，求实数的取值范围.

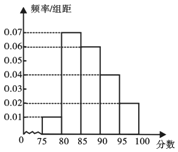
【题目】某手机生产企业为了解消费者对某款手机的认同情况，通过销售部随机抽取50名购买该款手机的消费者，并发出问卷调查(满分50分），该问卷只有20份给予回复，这20份的评分如下：

男

47,36,28,48,48,44,50,46,50,37,35,49

女

38,37,50,36,38,45,29,39

（1）完成下面的茎叶图，并求12名男消费者评分的中位数与8名女消费者评分的众数及平均值；

男

女

2

3

4

5

满意

不满意

合计

男

女

合计

（2）若大于40分为“满意”，否则为“不满意”，完成上面的列联表，并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关；

（3）若从回复的20名消费者中按性别用分层抽样的方法抽取5人，再从这5人中随机抽取2人作进一步调查，求至少有1名女性消费者被抽到的概率．

附：

0.05

0.025

0.01

3.841

5.024

6.635

【题目】已知函数的定义域为，部分对应值如下表．

x

0

4

5

1

2

2

1

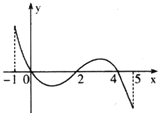
的导函数的图象如图所示：下列关于的命题：

函数是周期函数；

函数在是减函数；

如果当时，的最大值是2，那么t的最大值为4；

函数的零点个数可能为0、1、2、3、4个．

其中正确命题的序号是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网