题目内容
【题目】六个人按下列要求站成一排，分别有多少种不同的站法？
（1） 甲不站在两端； （2） 甲 ，乙必须相邻；
（3）甲 ，乙不相邻. (4) 甲 ，乙之间恰有两人
【答案】(1)480.(2)240(3)480(4)144.
【解析】
（1）现在中间的4个位中选一个，排上甲，再其余的人任意排，即可求解；
（2）把甲、乙看成一个整体，进行全排列，即可求解；
（3）先把甲、乙二人单独挑出，然后再把甲、乙插入其余4人形成的5个空中，即可求解；
（4）先把甲、乙排好，再从其余的4人中选出2人放到甲、乙中间，最后把排好的这4个人看做一个整体进行排列，即可求解．
（1）现在中间的4个位中选一个，排上甲，方法有4种，其余的人任意排，方法有
（种）；
（2）把甲、乙看成一个整体，这样6个人变成了5个人，全排列方法共有
（种）；
（3）先把甲、乙二人单独挑出来，把其余的4个人全排列，然后再把甲、乙插入其余4人形成的5个空中，方法共有
（种）；
（4）先把甲、乙排好，有
种方法，再从其余的4人中选出2人放到甲、乙中间，方法有
种.
把排好的这4个人看做一个整体，再与其他的2个人进行排列，方法有
种.
根据分步计数原理，求得甲、乙之间间隔两人的排法共有
（种）；
【题目】若某产品的直径长与标准值的差的绝对值不超过1mm 时，则视为合格品，否则视为不合格品。在近期一次产品抽样检查中，从某厂生产的此种产品中，随机抽取5000件进行检测，结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差（单位：mm）, 将所得数据分组，得到如下频率分布表：
分组 | 频数 | 频率 |
[-3, -2) |
| 0.10 |
[-2, -1) | 8 |
|
（1,2] |
| 0.50 |
（2,3] | 10 |
|
（3,4] |
|
|
合计 | 50 | 1．00 |
（Ⅰ）将上面表格中缺少的数据填在答题卡的相应位置；
（Ⅱ）估计该厂生产的此种产品中，不合格品的直径长与标准值的差落在区间（1,3]内的概率；
（Ⅲ）现对该厂这种产品的某个批次进行检查，结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
【题目】某种产品的质量按照其质量指标值M进行等级划分，具体如下表：
质量指标值M |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
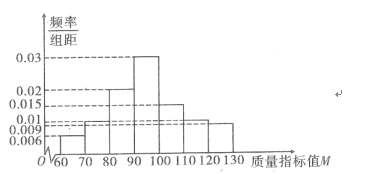
现从某企业生产的这种产品中随机抽取了100件作为样本，对其质量指标值M进行统计分析，得到如图所示的频率分布直方图.
（1）记A表示事件“一件这种产品为二等品或一等品”，试估计事件A的概率；
（2）已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元，试估计该企业销售10000件该产品的利润；
（3）根据该产品质量指标值M的频率分布直方图，求质量指标值M的中位数的估计值（精确到0.01）
