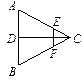题目内容
(本小题满分14分)
如图,在三棱柱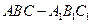 中,每个侧面均为正方形,
中,每个侧面均为正方形,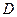 为底边
为底边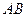 的中点,
的中点,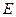 为侧棱
为侧棱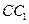 的中点.
的中点.
(Ⅰ)求证: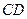 ∥平面
∥平面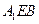 ;
;
(Ⅱ)求证: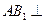 平面
平面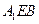 ;
;
(Ⅲ)求直线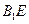 与平面
与平面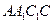 所成角的正弦值.
所成角的正弦值. 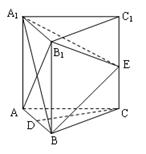
如图,在三棱柱
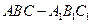 中,每个侧面均为正方形,
中,每个侧面均为正方形,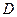 为底边
为底边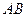 的中点,
的中点,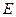 为侧棱
为侧棱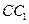 的中点.
的中点.(Ⅰ)求证:
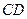 ∥平面
∥平面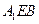 ;
;(Ⅱ)求证:
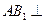 平面
平面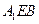 ;
;(Ⅲ)求直线
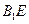 与平面
与平面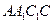 所成角的正弦值.
所成角的正弦值. 
(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)直线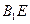 与平面
与平面 所成角的正弦值为
所成角的正弦值为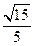
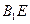 与平面
与平面 所成角的正弦值为
所成角的正弦值为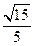
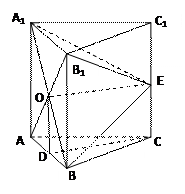 证明:(Ⅰ)设
证明:(Ⅰ)设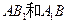 的交点为O,连接
的交点为O,连接 ,连接
,连接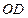 .
.
因为
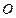 为
为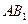 的中点,
的中点,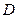 为
为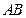 的中点,
的中点,所以
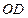 ∥
∥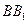 且
且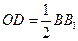 .又
.又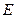 是
是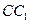 中点,
中点,所以
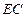 ∥
∥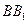 且
且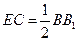 ,
,所以
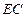 ∥
∥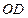 且
且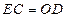 .
.所以,四边形
 为平行四边形.所以
为平行四边形.所以 ∥
∥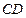 .
.又
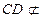 平面
平面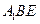 ,
,
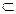 平面
平面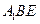 ,则
,则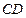 ∥平面
∥平面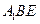 . ………………5分
. ………………5分(Ⅱ)因为三棱柱各侧面都是正方形,所以
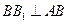 ,
,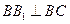 .
.所以
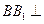 平面
平面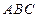 .
.因为
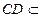 平面
平面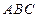 ,所以
,所以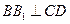 .
.由已知得
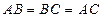 ,所以
,所以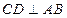 ,
,所以
 平面
平面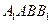 .
.由(Ⅰ)可知
 ∥
∥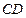 ,所以
,所以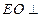 平面
平面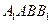 .
.所以
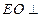
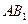 .
.因为侧面是正方形,所以
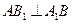 .
.又
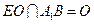 ,
,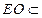 平面
平面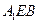 ,
,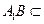 平面
平面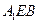 ,
,所以
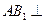 平面
平面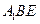 . ………………………………………10分
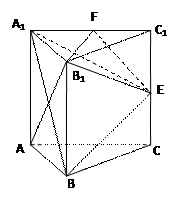
. ………………………………………10分(Ⅲ)解: 取
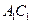 中点
中点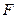 ,连接
,连接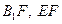 .
. 在三棱柱
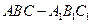 中,因为
中,因为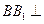 平面
平面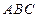 ,
, 所以侧面
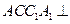 底面
底面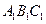 .
.因为底面
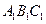 是正三角形,且
是正三角形,且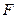 是
是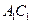 中点,
中点,所以
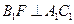 ,所以
,所以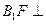 侧面
侧面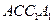 .
.所以
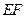 是
是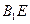 在平面
在平面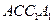 上的射影.
上的射影.所以
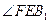 是
是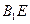 与平面
与平面 所成角.
所成角.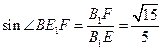 . …………………………………………14分
. …………………………………………14分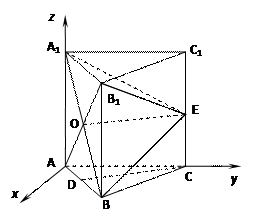 解法二:如图所示,建立空间直角坐标系.
解法二:如图所示,建立空间直角坐标系.设边长为2,可求得
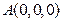 ,
,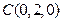 ,
,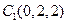 ,
,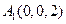 ,
,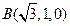 ,
,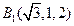 ,
,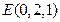 ,
,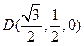 ,
,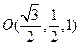 .
.(Ⅰ)易得,
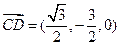 ,
,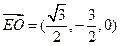 . 所以
. 所以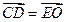 ,所以
,所以 ∥
∥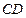 .
.又
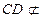 平面
平面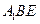 ,
,
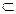 平面
平面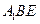 ,则
,则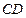 ∥平面
∥平面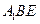 . ………………5分
. ………………5分(Ⅱ)易得,
 ,
,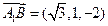 ,
,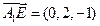
所以
 .
.所以
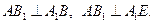
又因为
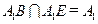 ,
,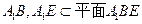 ,
,所以
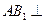 平面
平面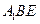 . …………………………………………… 10分
. …………………………………………… 10分(Ⅲ)设侧面
 的法向量为
的法向量为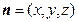 ,
,因为
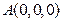 ,
, 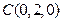 ,
,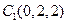 ,
,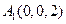 ,
,所以
 ,
,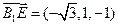 .
.由
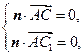 得
得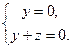 解得
解得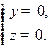
不妨令
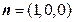 ,设直线
,设直线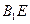 与平面
与平面 所成角为
所成角为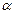 .
.所以
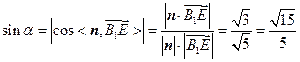 .
.所以直线
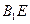 与平面
与平面 所成角的正弦值为
所成角的正弦值为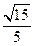 .………………………14分
.………………………14分
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 公垂线段
公垂线段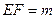 ,线段
,线段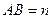 ,
,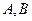 分别在
分别在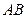 中点轨迹
中点轨迹 的三视图如图所示,
的三视图如图所示, ,A1A=
,A1A= ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, 在线段
在线段 上且
上且 =
= .
. ⊥平面
⊥平面 ;
; 的余弦值.
的余弦值.
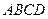 和矩形
和矩形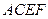 所在的平面互相垂直,
所在的平面互相垂直,
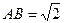 ,
,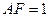 ,
,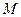 是线段
是线段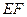 的中点.
的中点.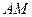 ∥平面
∥平面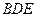 ;
;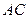 上确定一点
上确定一点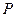 ,使得
,使得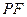 与
与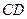 所成的角是
所成的角是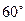 .
.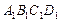 中,AB=BC=4,
中,AB=BC=4,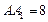 ,E为
,E为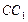 的中点,
的中点,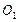 为下底面正方形的中心.求:(I)二面角C—AB—
为下底面正方形的中心.求:(I)二面角C—AB—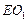 所成角的正切值;
所成角的正切值;
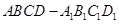 ,的棱长为1,
,的棱长为1,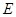 为
为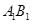 的中点,则下列五个命题:
的中点,则下列五个命题: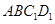 ,的距离为
,的距离为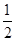
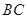 与平面
与平面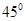
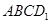 ,在正方体六个面内形成六个射影,其面积的最小值是
,在正方体六个面内形成六个射影,其面积的最小值是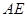 与
与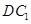 所成的角
所成的角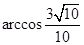
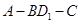 的大小为
的大小为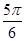
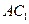 中
中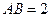 ,
,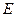 为
为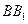 的中点.
的中点.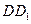 上确定一点F使
上确定一点F使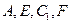 四点共面,并加以证明;
四点共面,并加以证明;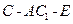 的平面角
的平面角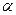 的余弦值;
的余弦值;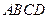 内,且点M在平面
内,且点M在平面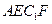 上的射影恰为
上的射影恰为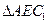 的重心,求异面直线
的重心,求异面直线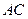 与
与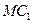 所成角的余弦值.
所成角的余弦值.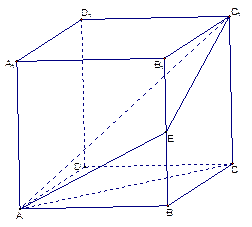
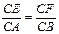 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).