题目内容
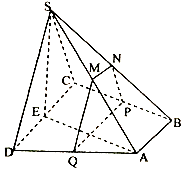
【题目】已知椭圆C: ![]() (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若 ![]()
![]() =0,
=0, ![]() =
= ![]() ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围.
【答案】
(1)
解:由题意可知:a=2,
令x=c,代入椭圆方程,解得:y= ![]() ,则丨PQ丨=
,则丨PQ丨= ![]() =3,
=3,
则b= ![]() ,
,
∴椭圆的标准方程为: ![]()
(2)
解:①当直线MN斜率不存在时,设lMN:x=m,
则 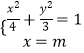 ,解得:y=
,解得:y= ![]() ,则丨MN丨=2
,则丨MN丨=2 ![]() ,
,
设直线MN与x轴交于点B,丨丨MB=丨AM丨即 ![]() =2﹣m,
=2﹣m,
∴m= ![]() 或m=2(舍),
或m=2(舍),
∴直线lMN过定点( ![]() ,0);
,0);
当直线MN斜率存在时,设直线MN斜率为k,
设M(x1,y1),N(x2,y2),则直线MN:y=kx+b,
与椭圆方程 ![]() ,联立,消取y整理得(4k2+3)x2+8kbx+4k2﹣12=0,
,联立,消取y整理得(4k2+3)x2+8kbx+4k2﹣12=0,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
△>0,k∈R,
![]()
![]() =0,(x1﹣2,y1)(x2﹣2,y2)=0,
=0,(x1﹣2,y1)(x2﹣2,y2)=0,
即x1x2﹣2(x1+x2)+4+y1y2=0,
y1y2=(kx1+b)(kx2+b)=k2x1x2+kb(x1+x2)+b2= ![]() ,
,
∴7b2+4k2+16kb=0,则b=﹣ ![]() k,或b=﹣2k,
k,或b=﹣2k,
∴lMN:y=k(x﹣ ![]() )或y=k(x﹣2),
)或y=k(x﹣2),
∴直线lMN过定点( ![]() ,0)或(2,0);
,0)或(2,0);
综合知,直线过定点( ![]() ,0);
,0);
②T为MN中点,T( ![]() ,
, ![]() ),则T(﹣
),则T(﹣ ![]() ,
, ![]() ),
),
∴kAT= 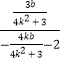 =
= ![]() ,
,
由b=﹣ ![]() ,则kAT=
,则kAT= ![]() ,
,
当k=0时,kAT=0,
当k≠0时,k∈R,kAT= ![]() =
= ![]() ,
,
由8k+ ![]() ≥2
≥2 ![]() =2
=2 ![]() ,
,
或8k+ ![]() ≤﹣2
≤﹣2 ![]() =﹣2
=﹣2 ![]() ,
,
∴kAT∈[﹣ ![]() ,
, ![]() ],
],
直线AT的斜率的取值范围为[﹣ ![]() ,
, ![]() ]
]
【解析】(1)由a=2,则椭圆的通径丨PQ丨= ![]() ,代入即可求得b的值,即可取得椭圆的方程;(2)当直线MN斜率不存在时,将x=m代入椭圆方程,则
,代入即可求得b的值,即可取得椭圆的方程;(2)当直线MN斜率不存在时,将x=m代入椭圆方程,则 ![]() =2﹣m,即可求得m的值,即可求得直线恒过定点;当斜率存在,设直线方程y=kx+b,代入椭圆方程,由韦达定理,向量的坐标运算,即可求得b=﹣
=2﹣m,即可求得m的值,即可求得直线恒过定点;当斜率存在,设直线方程y=kx+b,代入椭圆方程,由韦达定理,向量的坐标运算,即可求得b=﹣ ![]() k,或b=﹣2k,即可求得直线方程,则直线过定点(
k,或b=﹣2k,即可求得直线方程,则直线过定点( ![]() ,0);(3)利用中点坐标公式求得T坐标,利用直线的斜率公式,kAT=
,0);(3)利用中点坐标公式求得T坐标,利用直线的斜率公式,kAT= ![]() =
= ![]() ,分类当k=0,kAT=0,当k≠0时,利用基本不等式的性质,即可求得直线AT的斜率的取值范围.
,分类当k=0,kAT=0,当k≠0时,利用基本不等式的性质,即可求得直线AT的斜率的取值范围.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

【题目】某服装批发市场1-5月份的服装销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这五个月的利润中任选2个,分别记为![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想.参考公式:  .
.
【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据,通过计算统计量K2= ![]() ,并参考一下临界数据:
,并参考一下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01
【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 45 | 75 | 90 | 60 | 30 |
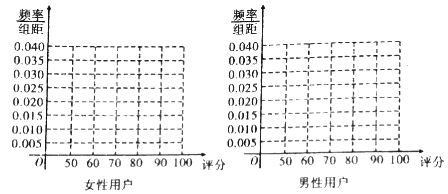
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.