��Ŀ����
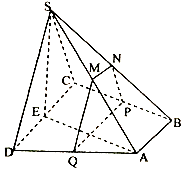
����Ŀ����ͼ������S��ABCD�У�����ABCDΪֱ�����Σ�AB��CD��BC��CD��ƽ��SCD��ƽ��ABCD��SC=SD=CD=AD=2AB��M��N�ֱ�ΪSA��SB���е㣬EΪCD�е㣬��M��N��ƽ��MNPQ�ֱ���BC��AD���ڵ�P��Q���� ![]() =t
=t ![]() ��
�� 
��1����t= ![]() ʱ����֤��ƽ��SAE��ƽ��MNPQ��
ʱ����֤��ƽ��SAE��ƽ��MNPQ��
��2���Ƿ����ʵ��t��ʹ�ö����M��PQ��A��ƽ��ǵ�����ֵΪ ![]() �������ڣ����ʵ��t��ֵ���������ڣ�˵�����ɣ�
�������ڣ����ʵ��t��ֵ���������ڣ�˵�����ɣ�
���𰸡�
��1��֤������1��EΪCD�е㣬���ı���ABCEΪ���Σ�
��AE��CD��
��t= ![]() ʱ��QΪAD�е㣬PQ��CD������PQ��AE��
ʱ��QΪAD�е㣬PQ��CD������PQ��AE��
��ƽ��SCD��ƽ��ABCD��SE��CD����SE����ABCD��
��PQ��ABCD����PQ��SE����PQ����SAE��
������MNPQ����SAE
��2���⣺��ͼ����EΪԭ�㣬ED��EA��ESֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ����ͼ��ʾ����ϵ��
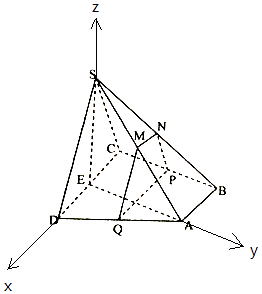
��ED=a����M����1��t��a���� ![]() ��
�� ![]() ��a��
��a�� ![]() a����E��0��0��0����A��0��
a����E��0��0��0����A��0�� ![]() ��0����
��0����
Q����1��t��a�� ![]() ��0����
��0���� ![]() =��0��
=��0�� ![]() ��
�� ![]() ����
����
��ABCDһ����������Ϊ ![]() =��1��0��0����
=��1��0��0����
��ƽ��MPQ�ķ����� ![]() =��x��y��z����
=��x��y��z����
��  ��ȡz=2����
��ȡz=2���� ![]() =��0��
=��0�� ![]() ��2����
��2����
ƽ��ABCD�ķ�����Ϊ ![]() =��0��0��1��
=��0��0��1��
�߶����M��PQ��A��ƽ��ǵ�����ֵΪ ![]() ��
��
�������⣺cos��= ![]() =
= 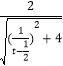 =
= ![]() ��
��
���t= ![]() ��t=
��t= ![]() ��
��
��ͼ��֪����t= ![]() ʱ�������M��PQ��AΪ�۶���ǣ��������⣬��ȥ
ʱ�������M��PQ��AΪ�۶���ǣ��������⣬��ȥ
���ϣ�t= ![]() ��
��
����������1���Ƶ���AE��CD��PQ��AE���Ӷ�SE����ABCD���ɴ���֤����MNPQ����SAE����2����EΪԭ�㣬ED��EA��ESֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ���ռ�ֱ������ϵ�����������������t��ֵ��

