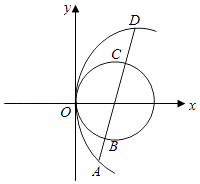
题目内容
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且
,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且 ![]() .
.
(1)求椭圆E的方程;
(2)求证:2m2=4k2+3;
(3)求|AB|的最大值.
【答案】
(1)解:由题意可得: ![]() ,a=2,a2=b2+c2,解得a=2,c=1,b2=3.
,a=2,a2=b2+c2,解得a=2,c=1,b2=3.
∴椭圆E的方程为 ![]() =1
=1
(2)证明:设A(x1,y1),B(x2,y2),
联立 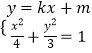 ,化为:(3+4k2)x2+8kmx+4m2﹣12=0,
,化为:(3+4k2)x2+8kmx+4m2﹣12=0,
△>0,∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∵ ![]() .
.
∴ ![]() =﹣
=﹣ ![]() ,即3x1x2+4y1y2=0,
,即3x1x2+4y1y2=0,
∴3x1x2+4(kx1+m)(kx2+m)=0,
化为:(3+4k2)x1x2+4km(x1+x2)+4m2=0,
∴(3+4k2) ![]() +4km
+4km ![]() +4m2=0,
+4m2=0,
化为:2m2=4k2+3
(3)解:由(2)可得:△=64k2m2﹣4(3+4k2)(4m2﹣12)>0,
化为:4k2+3>m2,∴4k2+3 ![]() ,∴k∈R.
,∴k∈R.
|AB|= ![]()
= ![]()
= ![]()
= ![]() =
= ![]() ∈
∈ ![]() .
.
当且仅当k=0时,|AB|的最大值2 ![]()
【解析】(1)根据椭圆的基本性质解题;(2)本小题主要应用了根与系数的关系来化简计算过程;(3)先根据(2)判断点A,点B的存在性,再根据两点间的距离公式线段AB长的表达式,最后求得线段AB的最大值.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 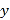 ,
, ![]() .
.
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);

(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?