Question

【题目】把一枚质地均匀的骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组

(1)求方程组只有一个解的概率;

(2)若方程组每个解对应平面直角坐标系中的点P(x,y),求点P落在第四象限的概率.

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）利用列举法求出基本事件，设方程组只有一个解为事件，则事件的对立事件是方程组无解或有无数多组解，由此利用对立事件概率计算公式能求出方程组只有一个解的概率；（2）设点落在第四象限为事件，利用列举法求出符合条件的数组的个数，由此能求出点落在第四象限的概率．

试题解析：点(a,b)所有可能出现的结果有

(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),

(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),

(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),

(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),

(5,1),(5,2),(5,3),(5,4)(5,5),(5,6),

(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种.

(1)“方程组只有一个解”记为事件A,其对立事件为该方程组无解或有无数多组解,则,即a=2b,此时有(2,1),(4,2),(6,3)3个点满足,

所以,P(A)=1-.

(2)“点P(x,y)落在第四象限”记为事件B,

由方程组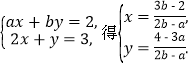若点P落在第四象限,则有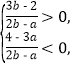

当2b-a>0,即b>时, 则，即

所以符合条件的点(a,b)有(2,2),(2,3),(3,2),(3,3),(3,4),(3,5),(4,2),(4,3),(4,4),(4,5),(4,6),(5,2),(5,3),(5,4),(5,5),(5,6),(6,2),(6,3),(6,4),(6,5),(6,6),共21个.当2b-a<0,即b<时,则，不存在符合条件的点(a,b).

所以,P(B)=.