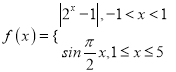题目内容
【题目】已知![]()
(I)判断f(x)的奇偶性并证明
(Ⅱ)若a>1,判断f(x)的单调性并用单调性定义证明;
(Ⅲ)若![]() ,求实数x的取值范围
,求实数x的取值范围
【答案】(I)见解析;(II) 见解析;(III) ![]()
【解析】试题分析:(1)求解![]() 即可.
即可.
(2)运用单调性证明则f(x1)-f(x2)=loga![]() -loga
-loga![]() =loga
=loga![]() .判断符号即可.
.判断符号即可.
(3)根据单调性转化-1<x-3≤![]() 求解.
求解.
试题解析:(I)由![]() 得
得![]() ,∴函数f(x)的定义域为(-1,1) 关于原点对称.
,∴函数f(x)的定义域为(-1,1) 关于原点对称.
f(x)在(-1,1)上为奇函数,证明如下:
![]() ,
,
∴f(x)为(-1,1)上的奇函数.
(II) 若![]() ,f(x)在(-1,1)上单调递增,证明如下:
,f(x)在(-1,1)上单调递增,证明如下:
设-1<x1<x2<1, ![]()
则f(x1)-f(x2)=loga![]() -loga
-loga![]() =loga
=loga![]() .
.
又-1<x1<x2<1,
∴(1+x1)(1-x2)-(1-x1)(1+x2)=2(x1-x2)<0,
即0<(1+x1)(1-x2)<(1-x1)(1+x2),
∴0<![]() <1,∴loga
<1,∴loga![]() <0,
<0,
∴f(x1)<f(x2),∴f(x)在(-1,1)上单调递增.
(III)∵f(x)为(-1,1)上的奇函数,
∴f(x-3) ≤-f(-![]() )=f(
)=f(![]() ).
).
若![]() ,f(x)在(-1,1)上单调递增,
,f(x)在(-1,1)上单调递增,
∴-1<x-3≤![]() ,得2<x≤
,得2<x≤![]() .
.
若![]() ,f(x)在(-1,1)上单调递减,
,f(x)在(-1,1)上单调递减,
∴![]() ≤x-3<1,得
≤x-3<1,得![]() ≤x<4.
≤x<4.
综上可知,当![]() 时,实数x的取值范围为
时,实数x的取值范围为![]() ;
;
当![]() 时,实数x的取值范围为
时,实数x的取值范围为![]()
点晴:本题属于对函数单调性应用的考察,若函数![]() 在区间上单调递增,则
在区间上单调递增,则![]() 时,有
时,有![]() ,事实上,若
,事实上,若![]() ,则
,则![]() ,这与
,这与![]() 矛盾,类似地,若
矛盾,类似地,若![]() 在区间上单调递减,则当
在区间上单调递减,则当![]() 时有
时有![]() ;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中的易错点是容易忽视定义域(-1,1).
;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中的易错点是容易忽视定义域(-1,1).

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目