题目内容
4.已知正四棱台底面边长分别为20cm和10cm,侧面积为780cm2,求其体积.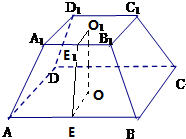
分析 利用已知条件求出棱台的斜高,然后求出高,利用棱台的体积公式求出体积即可.
解答 解:正四棱台底面边长分别为20cm和10cm,侧面积为780cm2,设h′为了的斜高,
可得780=4×$\frac{20+10}{2}•h′$,解得h′=13.
即EE1=13,
∴棱台的高OO1=$\sqrt{{EE}_{1}{\;}^{2}-(EO-{E}_{1}{O}_{1})^{2}}$=$\sqrt{{13}^{2}-{5}^{2}}$=12.
∴V=$\frac{1}{3}$h[S+S′+$\sqrt{SS′}$]=$\frac{1}{3}×12×({10}^{2}+{20}^{2}+10×20)$=2800cm3
棱台的体积为:2800cm3
点评 本题是中档题,考查棱台的有关知识,考查空间想象能力,计算能力,正确应用棱台的体积公式,常考题型.

练习册系列答案
相关题目
15.如表给出了甲、乙、丙三种食品的维生素A,B的含量及成本:
营养师想购买这三种食品共10kg,使其维生素A不少于4400单位,维生素B不少于4800单位,问:三种食品各购多少时,既能满足上述条件,又能使成本最低?最低成本是多少?
| 甲 | 乙 | 丙 | |
| A(单位/千克) | 400 | 600 | 400 |
| B(单位/千克) | 800 | 200 | 400 |
| 成本 | 7 | 6 | 5 |