题目内容
16.甲、乙、丙、丁站成一排,其中要求甲左乙右(可以不相邻),有多少种不同的排法?分析 根据题意,首先利用排列数公式计算甲、乙、丙、丁站成一排的排法数目,进而分析可得“甲左乙右”和“甲右乙左”的情况数目相等,即可得甲左乙右的排法是全部排法数目的$\frac{1}{2}$,计算可得答案.
解答 解:根据题意,甲、乙、丙、丁站成一排,有A44=24种情况,
其中甲左乙右和甲右乙左的情况数目相等,
则甲左乙右的排法有$\frac{1}{2}$×24=12种;
故甲、乙、丙、丁站成一排,甲左乙右的排法有12种.
点评 本题考查排列、组合的运用,关键是明确“甲左乙右”和“甲右乙左”的情况数目相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.记f(x)=$\frac{1+x}{1-x}$,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2015(x)=( )
| A. | -$\frac{1}{x}$ | B. | x | C. | $\frac{x-1}{x+1}$ | D. | $\frac{1+x}{1-x}$ |
9.已知实数x,y满足方程x2+y2-4x+1=0,求:
(1)$\frac{y}{x}$的最大值和最小值;
(2)y-x的最小值;
(3)x2+y2的最大值和最小值;
(4)2x2+y2-4x-6的最大值.
(1)$\frac{y}{x}$的最大值和最小值;
(2)y-x的最小值;
(3)x2+y2的最大值和最小值;
(4)2x2+y2-4x-6的最大值.
10.下列说法错误的是 ( )
| A. | 平面直角坐标系内,每一条直线都有一个确定的倾斜角 | |
| B. | 每一条直线的斜率都是一个确定的值 | |
| C. | 没有斜率的直线是存在的 | |
| D. | 同一直线的斜率与倾斜角不是一一对应的 |
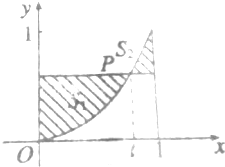 如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.
如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.