题目内容
19.已知椭圆x28+y24x28+y24=1,求斜率为2的弦中点M的轨迹方程.分析 设出弦的中点M,端点A,B的坐标,通过三点坐标的关系,把A,B的坐标代入椭圆方程后作差,代入直线l的斜率整理后即可得到答案;
解答 解:设斜率为2的弦中点M(x,y),A(x1,y1),B(x2,y2).
∵M为弦AB的中点,∴x1+x2=2x,y1+y2=2y.
则x128+y124=1x128+y124=1,①
x228+y224=1x228+y224=1,②
②-①得,y2−y1x2−x1y2−y1x2−x1=-1212×x2+x1y2+y1x2+x1y2+y1.
∴−x2y=2−x2y=2,整理得:x+4y=0.
由{x28+y24=1x+4y=0{x28+y24=1x+4y=0,解得x=±83±83
所求轨迹方程为:x+y=0.(-8383<x<8383)
∴点P的轨迹方程为:x+4y=0(-8383<x<8383);
点评 本题考查了直线与圆锥曲线的关系,训练了“点差法”,涉及中点弦问题.利用点差法能起到事半功倍的作用,该题是中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
11.记f(x)=1+x1−x,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2015(x)=( )
| A. | -1x | B. | x | C. | x−1x+1 | D. | 1+x1−x |
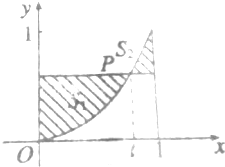 如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.
如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.