题目内容

11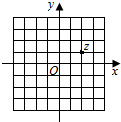．若i为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z表示复数z，那么复数$\frac{z}{1+i}$对应的点位于复平面内的（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 由图求得z，代入$\frac{z}{1+i}$后利用复数代数形式的乘除运算化简得答案．

解答 解：由图知，z=2+i，
∴$\frac{z}{1+i}=\frac{2+i}{1+i}=\frac{（2+i）（1-i）}{（1+i）（1-i）}=\frac{3-i}{2}=\frac{3}{2}-\frac{1}{2}i$，
则对应的点的坐标为（$\frac{3}{2}，-\frac{1}{2}$），位于复平面内的第四象限．
故选：D．

点评 本题考查了复数的代数表示法及其几何意义，考查了复数代数形式的乘除运算，是基础题．

练习册系列答案
相关题目
1．在直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}{x=1+cosφ}\\{y=sinφ}\end{array}\right.$（φ为参数，0≤φ≤π）．以O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C与θ=$\frac{π}{3}$（ρ＞0）所表示的图形的交点的直角坐标是$（\frac{1}{2}，\frac{\sqrt{3}}{2}）$．
2．将函数y=sin（2x+$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$个单位，再纵坐标不变，横坐标变为原来的2倍，所得新图象的函数解析式是（　　）
A．y=sin4xB．y=sinxC．y=sin（4x-$\frac{π}{6}$）D．y=sin（x-$\frac{π}{6}$）
19．在直角坐标平面内，曲线C的参数方程为$\left\{\begin{array}{l}x=rcosα\\ y=rsinα\end{array}\right.$（r＞0，α为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知点A、B的极坐标分别为$（2\;，\;\frac{2π}{3}）$、（2，π），若直线AB和曲线C只有一个公共点，则r=$\sqrt{3}$．
6．设F1、F2是椭圆x2+$\frac{{y}^{2}}{{b}^{2}}$=1（0＜b＜1）的左、右焦点，过F1的直线l交椭圆于A，B两点，若|AF1|=3|F1B|，且AF2⊥x轴，则b2=（　　）
A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{3}{4}$
16．在△ABC中，a，b，c分别是角A、B、C的对边，且$\frac{cosB}{cosC}=-\frac{b}{2a+c}$．
（Ⅰ）求角B的大小；
（Ⅱ）若△ABC的面积S=$\sqrt{3}$，a=1，求边AC上的中线BD的长．
3．直线ax+by-a=0与圆x2+y2+2x-4=0的位置关系是（　　）
A．相离B．相切C．相交D．与a，b的取值有关
20．若复数1-$\sqrt{3}i$（i为虚数单位），是z的共轭复数，则在复平面内，复数z对应的点的坐标为（　　）
A．（0，1）B．（1，-$\sqrt{3}$）C．（-1，-$\sqrt{3}$）D．（-1，0）
1．直线l过抛物线y2=x的焦点F，交抛物线于A、B两点，且点A在x轴上方．若直线l的倾斜角θ≥$\frac{π}{4}$，则|FA|的取值范围是（$\frac{1}{4}$，1+$\frac{\sqrt{2}}{2}$]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网