题目内容
【题目】若不等式x2+2ax+1≥0对于一切x∈（0， 
]成立，则a的最小值是 ．
【答案】- 
【解析】解：当x∈（0， 
]时，
不等式x2+2ax+1≥0可化为a≥﹣ x﹣ 
，
设f（x）=﹣ x﹣ ，x∈（0， ]，
且函数f（x）在x∈（0， ]上是单调增函数，
最大值是f（ ）=﹣ × ﹣ 
=﹣ ，
∴a的最小值是﹣ ．
所以答案是：- ．
【考点精析】本题主要考查了解一元二次不等式的相关知识点，需要掌握求一元二次不等式
解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边才能正确解答此题．
轻松暑假总复习系列答案
【题目】下表给出
三种食物的维生素含量及其成本：
|
|
| |
维生素A（单位/千克） | 4000 | 5000 | 300 |
维生素B（单位/千克） | 700 | 100 | 300 |
成本（元/千克） | 6 | 4 | 3 |
现欲将三种食物混合成本100千克的混合食品，要求至少含35000单位维生素A，40000单位维生素B，采用何种配比成本最小？
【题目】我校举行的 “青年歌手大选赛”吸引了众多有才华的学生参赛．为了了解本次比赛成绩情况，从中抽取了50名学生的成绩（得分取正整数，满分为100分）作为样本进行统计．请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图所示）解决下列问题：
组别 | 分组 | 频数 | 频率 |
第1组 | [50，60） | 8 | 0.16 |
第2组 | [60，70） | a | ▓ |
第3组 | [70，80） | 20 | 0.40 |
第4组 | [80，90） | ▓ | 0.08 |
第5组 | [90，100] | 2 | b |
合计 | ▓ | ▓ |
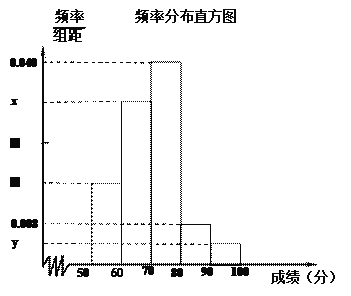
（1）求出
的值；
（2）在选取的样本中，从成绩是80分以上（含80分）的同学中随机抽取2名同学参加元旦晚会，求所抽取的2名同学中至少有1名同学来自第5组的概率；
（3）根据频率分布直方图，估计这50名学生成绩的众数、中位数和平均数。
