题目内容
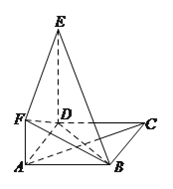
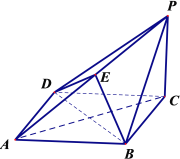
【题目】如图,在四棱锥![]() 中, 底面
中, 底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的体积的
的体积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】【试题分析】(1)借助题设条件运用线面垂直的判定定理推证;(2)借助线面平行的性质定理进行推证;(3)先假设存在,再借助线面的位置关系进行分析推证:
(Ⅰ)因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为底面![]() 是菱形,所以
是菱形,所以![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() .
.
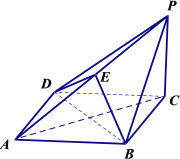
(Ⅱ)设![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() ,
,
因为平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,
又由![]() 是菱形可知
是菱形可知![]() 为
为![]() 中点,
中点,
所以,在![]() 中,
中,![]() ,
,
所以![]() .
.
(Ⅲ)在![]() 中过点
中过点![]() 作
作![]()
![]() ,交
,交![]() 于点
于点![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
由![]() 是菱形可知
是菱形可知![]() ,
,
假设存在点![]() 满足
满足![]() ,即
,即![]() ,则
,则
![]() ,
,
所以在![]() 中,
中,![]() ,
,
所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【题目】国Ⅳ标准规定:轻型汽车的屡氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量进行检测,检测结果记录如表(单位:mg/km)
A | 85 | 80 | 85 | 60 | 90 |
B | 70 | x | 95 | y | 75 |
由于表格被污损,数据x,y看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等,方差也相等.
(1)求表格中x与y的值;
(2)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为X,求X=1时的概率.