题目内容
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“![]() 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取
次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取![]() ,
,![]() )
)

A.16B.17C.24D.25
【答案】D
【解析】
由折线长度变化规律可知“![]() 次构造”后的折线长度为
次构造”后的折线长度为![]() ,由此得到
,由此得到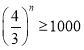 ,利用运算法则可知
,利用运算法则可知![]() ,由此计算得到结果.
,由此计算得到结果.
记初始线段长度为![]() ,则“一次构造”后的折线长度为
,则“一次构造”后的折线长度为![]() ,“二次构造”后的折线长度为
,“二次构造”后的折线长度为![]() ,以此类推,“
,以此类推,“![]() 次构造”后的折线长度为
次构造”后的折线长度为![]() ,
,
若得到的折线长度为初始线段长度的![]() 倍,则
倍,则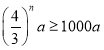 ,即
,即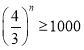 ,
,
 ,
,
即![]() ,
,![]() 至少需要
至少需要![]() 次构造.
次构造.
故选:![]() .
.

【题目】光农业科学研究所对冬季昼夜温差大小与反季节土豆发芽多少之间的关系进行分析研究,他们分别记录了11月1日至11月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如表资料:
日期 | 11月1日 | 11月2日 | 11月3日 | 11月4日 | 11月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 26 | 32 | 26 | 16 |
设农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是11月1日与11月5日的两组数据,请根据11月2日至11月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 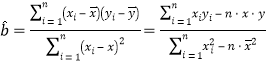 ,
,![]() )
)
【题目】已知直线![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和定点
和定点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一端点为点
直径的一个端点,若另一端点为点![]() ,问
,问![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【题目】某客户准备在家中安装一套净水系统,该系统为三级过滤,使用寿命为十年.如图所示,两个一级过滤器采用并联安装,二级过滤器与三级过滤器为串联安装。

其中每一级过滤都由核心部件滤芯来实现。在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立),三级滤芯无需更换,若客户在安装净水系统的同时购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.若客户在使用过程中单独购买滤芯,则一级滤芯每个
元.若客户在使用过程中单独购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据
元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据![]() 套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据
套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据![]() 个一级过滤器更换的滤芯个数制成的柱状图,表是根据
个一级过滤器更换的滤芯个数制成的柱状图,表是根据![]() 个二级过滤器更换的滤芯个数制成的频数分布表.
个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表
二级滤芯更换的个数 |
|
|
频数 |
|
|
以![]() 个一级过滤器更换滤芯的频率代替
个一级过滤器更换滤芯的频率代替![]() 个一级过滤器更换滤芯发生的概率,以
个一级过滤器更换滤芯发生的概率,以![]() 个二级过滤器更换滤芯的频率代替
个二级过滤器更换滤芯的频率代替![]() 个二级过滤器更换滤芯发生的概率.
个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为![]() 的概率;
的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() ,
,![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() ,
,![]() 的值.
的值.