题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数)在
为自然对数的底数)在![]() 上有两个零点,则
上有两个零点,则![]() 的范围是( )
的范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
利用参数分离法进行转化,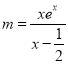 ,设
,设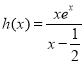 (
(![]() 且
且![]() ),
),
构造函数,求函数的导数,研究函数的单调性和极值,利用数形结合进行求解即可.
解:由![]() 得
得![]() ,
,
当![]() 时,方程不成立,即
时,方程不成立,即![]() ,
,
则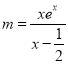 ,
,
设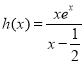 (
(![]() 且
且![]() ),
),
则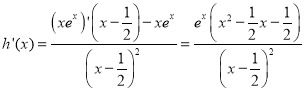
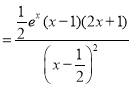 ,
,
∵![]() 且
且![]() ,∴由
,∴由![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,函数为增函数,
,函数为增函数,
当![]() 且
且![]() 时,
时,![]() ,函数为减函数,
,函数为减函数,
则当![]() 时函数取得极小值,极小值为
时函数取得极小值,极小值为![]() ,
,
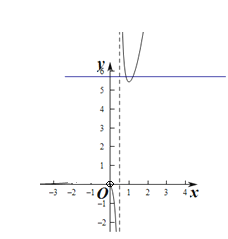
当![]() 时,
时,![]() ,且单调递减,作出函数
,且单调递减,作出函数![]() 的图象如图:
的图象如图:
要使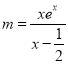 有两个不同的根,
有两个不同的根,
则![]() 即可,
即可,
即实数![]() 的取值范围是
的取值范围是![]() .
.
方法2:由![]() 得
得![]() ,
,
设![]() ,
,![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 为增函数,
为增函数,
设![]() 与
与![]() ,相切时的切点为
,相切时的切点为![]() ,切线斜率
,切线斜率![]() ,
,
则切线方程为![]() ,
,
当切线过![]() 时,
时,![]() ,
,
即![]() ,即
,即![]() ,得
,得![]() 或
或![]() (舍),则切线斜率
(舍),则切线斜率![]() ,
,
要使![]() 与
与![]() 在
在![]() 上有两个不同的交点,则
上有两个不同的交点,则![]() ,
,
即实数![]() 的取值范围是
的取值范围是![]() .
.
故选:D.


练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目