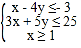题目内容
【题目】已知直线![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和定点
和定点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一端点为点
直径的一个端点,若另一端点为点![]() ,问
,问![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)先求出直线![]() 过定点
过定点![]() ,设圆的一般方程,由题意列方程组,即可求圆的方程;
,设圆的一般方程,由题意列方程组,即可求圆的方程;
(2)由(1)可知:求得直线![]() 的斜率,根据对称性求得点
的斜率,根据对称性求得点![]() 坐标,由
坐标,由![]() 在圆外,所以点
在圆外,所以点![]() 不能作为直角三角形的顶点,分类讨论,即可求得
不能作为直角三角形的顶点,分类讨论,即可求得![]() 的值.
的值.
(1)直线![]() 的方程可化为
的方程可化为![]() ,由
,由![]() 解得
解得![]()
∴定点![]() 的坐标为
的坐标为![]() . 设圆
. 设圆![]() 的方程为
的方程为![]() ,则圆心
,则圆心![]()
则依题意有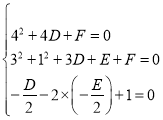 解得
解得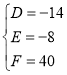
∴圆![]() 的方程为
的方程为![]() ;
;
(2)由(1)知圆![]() 的标准方程为
的标准方程为![]() ,∴圆心
,∴圆心![]() ,半径
,半径![]() .
.
∵![]() 是直径的两个端点,∴圆心
是直径的两个端点,∴圆心![]() 是
是![]() 与
与![]() 的中点,
的中点,![]()
∵![]() 轴上的点
轴上的点![]() 在圆外,∴
在圆外,∴![]() 是锐角,即
是锐角,即![]() 不是直角顶点.
不是直角顶点.
若![]() 是
是![]() 的直角顶点,则
的直角顶点,则![]() ,得
,得![]() ;
;
若![]() 是
是![]() 的直角顶点,则
的直角顶点,则![]() ,得
,得![]() .
.
综上所述,在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 为直角三角形,
为直角三角形,![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】(1)从某厂生产的一批零件1000个中抽取20个进行研究,应采用什么抽样方法?
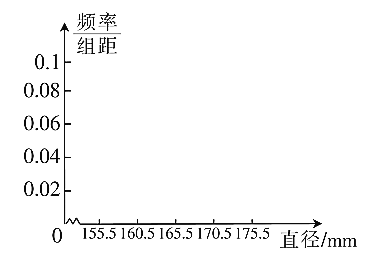
(2)对(1)中的20个零件的直径进行测量,得到下列不完整的频率分布表:(单位:mm)
分组 | 频数 | 频率 |
| 2 | |
| 6 | |
| 8 | |
| ||
合计 | 20 | 1 |
①完成频率分布表;
②画出其频率分布直方图.