题目内容
【题目】已知
为直平行六面体.命题
为正方体；命题
的任意体对角线与其不相交的面对角线垂直.则命题
是命题
的（ ）条件 .
A. 充分不必要 B. 必要不充分 C. 充分必要 D. 既不充分也不必要
【答案】C
【解析】
充分性显然成立，下面证明必要性成立.
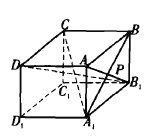
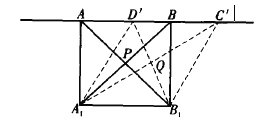
如下左图，上下底面为平行四边形，各个侧面均为矩形.
作体对角线
和
在平面
上的射影.
因为平面
平面
，所以，点
、
的垂足
、
必在直线
上，和在平面上的射影分别为
和
.平面上的图形如下右图.
由
，
，知四边形
是平行四边形，其对角线的交点为
.
又
，
，由三垂线定理知
，
.则
.
因为点到
的距离等于点
到的距离等于
，且是等腰
两腰上高的交点，所以，
也是等腰三角形.
从而，点与重合，且
.
故侧面是正方形.
同理，其他侧面四边形均为正方形.
又点、分别与
、
重合，由此可得底面四边形为正方形.
综上，六面体
为正方体.
故答案为：C
练习册系列答案
相关题目
