题目内容
(本小题15分)已知函数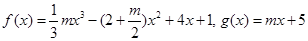 .
.
(1)当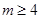 时,求
时,求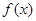 的单调递增区间;
的单调递增区间;
(2)是否存在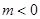 ,使得对任意的
,使得对任意的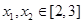 ,都有
,都有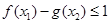 恒成立.若存在,求出
恒成立.若存在,求出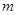 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.
(1) 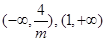 。(2)存在,
。(2)存在,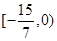
解析试题分析:(1)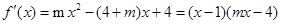
当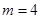 时,
时,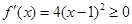 , ∴
, ∴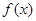 在
在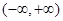 上单增, …………………2分
上单增, …………………2分
当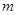 >4时,
>4时,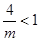 , ∴
, ∴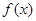 的递增区间为
的递增区间为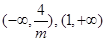 …….6.分
…….6.分
(2)假设存在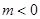 ,使得命题成立,此时
,使得命题成立,此时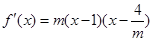 .
.
∵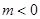 , ∴
, ∴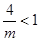 .
.
则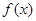 在
在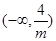 和
和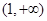 递减,在
递减,在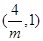 递增.
递增.
∴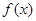 在[2,3]上单减,又
在[2,3]上单减,又 在[2,3]单减.
在[2,3]单减.
∴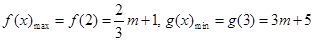 . …………………10分
. …………………10分
因此,对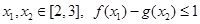 恒成立.
恒成立.
即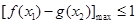 , 亦即
, 亦即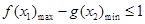 恒成立.
恒成立.
∴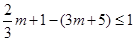 ∴
∴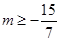 . 又
. 又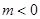 故
故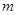 的范围为
的范围为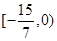 ...15分
...15分
考点:本题考查利用导数求函数的单调区间、导数在最大值、最小值问题中的应用及恒成立的问题。
点评:利用导数研究含参函数的单调区间,关键是解不等式,因此要研究含参不等式的解法,应注意对参数的讨论;研究是否存在问题,通常先假设存在,转化为封闭性问题,对于恒成立问题,一般应利用到函数的最值,而最值的确定又通常利用导数的方法解决.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
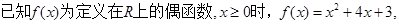
 时函数的解析式
时函数的解析式 上是单调递增
上是单调递增
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求: 的根为一正一负,则求实数
的根为一正一负,则求实数 内,则求实数
内,则求实数 ,
, 是
是 的一个极值点.
的一个极值点.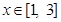 时,
时,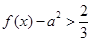 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.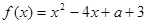 在区间
在区间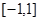 上存在零点;Q:函数
上存在零点;Q:函数 在
在 内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数
内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数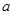 的取值范围.
的取值范围.
 ,
, ,使得
,使得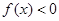 ,求实数
,求实数 的取值范围;
的取值范围; ,且
,且 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的函数
的函数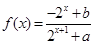 是奇函数
是奇函数  的解析式;
的解析式;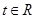 ,不等式
,不等式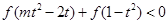 恒成立,求
恒成立,求 的取值范围.
的取值范围. 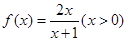
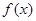 在
在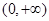 上为单调增函数;
上为单调增函数;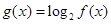 ,求
,求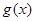 的值域;
的值域;  的方程
的方程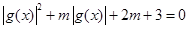 有三个不同的实数解,求
有三个不同的实数解,求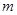 的取值范围.
的取值范围.