题目内容
(12分)已知函数 ,
, 是
是 的一个极值点.
的一个极值点.
(1)求 的单调递增区间;
的单调递增区间;
(2)若当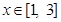 时,
时,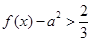 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅰ)函数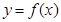 的单调递增区间为
的单调递增区间为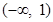 ,
,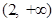 . (Ⅱ)
. (Ⅱ)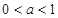 .
.
解析试题分析:(I)先求导函数,然后根据x=2是f(x)的一个极值点建立等式关系,求出b,然后解不等式f′(x)>0即可求出函数的单调增区间;
(II)先利用导数求出函数f(x)在区间[1,3]上的最小值,若当x∈[1,3]时,要使f(x)-a2> 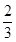
恒成立,只需f(x) min>a2+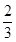 ,即可求出a的范围.
,即可求出a的范围.
解:(Ⅰ)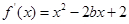 . ∵
. ∵ 是
是 的一个极值点,
的一个极值点,
∴ 是方程
是方程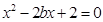 的一个根,解得
的一个根,解得 .
.
令 ,则
,则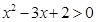 ,解得
,解得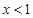 或
或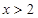 .
.
∴函数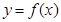 的单调递增区间为
的单调递增区间为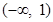 ,
,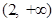 .
.
(Ⅱ)∵当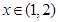 时
时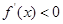 ,
,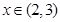 时
时 ,
,
∴ 在(1,2)上单调递减,
在(1,2)上单调递减, 在(2,3)上单调递增.
在(2,3)上单调递增.
∴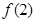 是
是 在区间[1,3]上的最小值,且
在区间[1,3]上的最小值,且 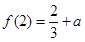 .
.
若当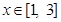 时,要使
时,要使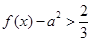 恒成立,只需
恒成立,只需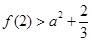 ,
,
即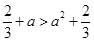 ,解得
,解得 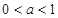 .
.
考点:本题主要考查了函数的极值,单调性和在闭区间上的最值,同时考查了恒成立问题,属于中档题
点评:解决该试题的关键是利用极值点处导数为零,那么得到参数b的值,然后求解二次不等式同时能将不等式的恒成立问题,转换为求解函数的最小值大于参数问题。即f(x) min>a2+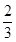 体现了转换与化归思想的和运用。
体现了转换与化归思想的和运用。

练习册系列答案
相关题目
 .
. 的值域为
的值域为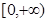 ,求a的值;
,求a的值; 上是增函数,求实数
上是增函数,求实数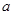 的取值范围.
的取值范围. 。
。 的定义域;
的定义域;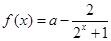 (其中常数
(其中常数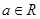 )
) 的单调性,并加以证明;
的单调性,并加以证明; 的值。
的值。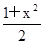 对一切实数x均成立?
对一切实数x均成立?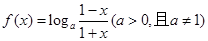
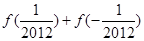 的值;
的值;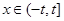 (其中
(其中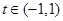 ,且
,且 为常数)时,
为常数)时,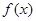 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如 时,求满足不等式
时,求满足不等式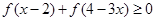 的
的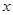 的范围.
的范围. 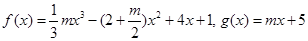 .
.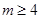 时,求
时,求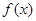 的单调递增区间;
的单调递增区间;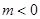 ,使得对任意的
,使得对任意的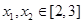 ,都有
,都有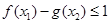 恒成立.若存在,求出
恒成立.若存在,求出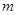 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由. 是定义在R上的减函数,且
是定义在R上的减函数,且 ,
,