题目内容
(本小题满分14分)已知定义域为 的函数
的函数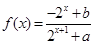 是奇函数
是奇函数
⑴求函数 的解析式;
的解析式;
⑵判断并证明函数 的单调性;
的单调性;
⑶若对于任意的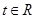 ,不等式
,不等式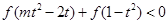 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)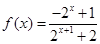 (2)减函数,证明见解析(3)
(2)减函数,证明见解析(3)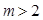
解析试题分析:⑴∵ 为奇函数,
为奇函数,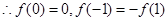
即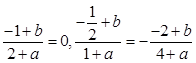 , 解得
, 解得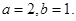
所以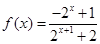 ,检验得
,检验得 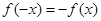 ,满足条件. …4分
,满足条件. …4分
⑵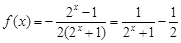 为
为 上的减函数
上的减函数
证明:设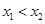
则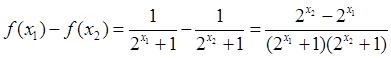
∵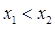
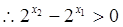 ,
, 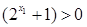
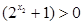

 即
即 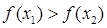

 为减函数 …8分
为减函数 …8分
⑶∵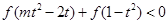 ,
, 
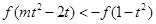
∵ 为奇函数,
为奇函数, ,
,
则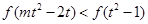 .
.
又 为减函数
为减函数 
 即
即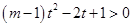 恒成立,
恒成立,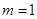 时显然不恒成立,
时显然不恒成立,
所以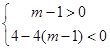
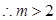 …14分
…14分
考点:本小题主要考查利用奇偶性求函数解析式,判断并证明函数的单调性,利用函数的单调性求解抽象不等式以及恒成立问题.
点评:如果奇函数在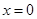 处有意义,则
处有意义,则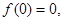 这一性质在解题时可以简化运算,特别好用,另外在用定义证明单调性时一定要把结果化到最简,尽量不要用已知函数的单调性来判断未知函数的单调性.解抽象不等式,关键是利用单调性“脱去”外层符号,得出具体的不等式,这一过程中要注意定义域是否有影响.
这一性质在解题时可以简化运算,特别好用,另外在用定义证明单调性时一定要把结果化到最简,尽量不要用已知函数的单调性来判断未知函数的单调性.解抽象不等式,关键是利用单调性“脱去”外层符号,得出具体的不等式,这一过程中要注意定义域是否有影响.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 。
。 的定义域;
的定义域;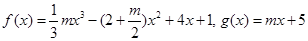 .
.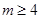 时,求
时,求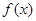 的单调递增区间;
的单调递增区间;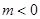 ,使得对任意的
,使得对任意的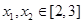 ,都有
,都有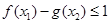 恒成立.若存在,求出
恒成立.若存在,求出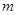 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由. ,函数
,函数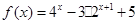 (其中
(其中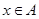 )
) 的定义域;
的定义域;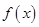 是定义在
是定义在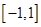 上的奇函数,且
上的奇函数,且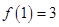 ,若
,若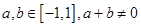 时,有
时,有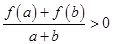 成立.
成立.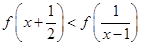 ;
;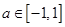 时,
时,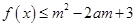 对所有的
对所有的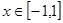 恒成立,求实数
恒成立,求实数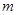 的取值范围.
的取值范围. .
. 的图像;
的图像; .
. 是定义在
是定义在 上的奇函数,当
上的奇函数,当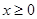 时,
时,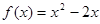 。
。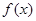 的解析式;
的解析式;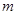 为何值时,方程
为何值时,方程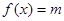 有三个解?
有三个解? 是定义在R上的减函数,且
是定义在R上的减函数,且 ,
,