题目内容
设P:二次函数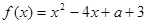 在区间
在区间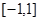 上存在零点;Q:函数
上存在零点;Q:函数 在
在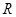 内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数
内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数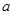 的取值范围.
的取值范围.
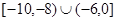 。
。
解析试题分析:先求出p,q为真时对应的a的取值范围,然后根据“P或Q”为真命题,“P且Q”为假命题确定p,q一真一假,从而分两种情况:p真q假或p假q真两种情况研究出a的取值范围,最后求并集即可.
因为函数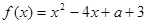 的对称轴是x=2,所以f(x)在区间[-1,1]上是减函数.又函数在区间[-1,1]上存在零点,则必有
的对称轴是x=2,所以f(x)在区间[-1,1]上是减函数.又函数在区间[-1,1]上存在零点,则必有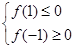 ,…………………2分
,…………………2分
即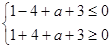 ,解得:
,解得: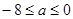 .
.
即P: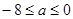 .
.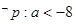 ,或
,或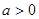 ………………………4分
………………………4分
又函数 在
在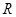 内没有极值点,则函数
内没有极值点,则函数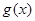 在
在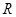 上是单调函数,而
上是单调函数,而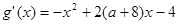 ,需
,需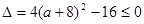 ,解得:
,解得: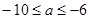
即Q: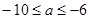 .
. Q:
Q: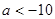 或
或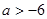 …………8分
…………8分
由题设“P或Q”为真命题,“P且Q”为假命题知:p、Q一真一假…………9分
①当p真Q假时,需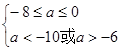 得:
得: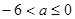 ………………10分
………………10分
②当p 假Q真时,需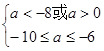 得:
得: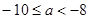 ………………12分
………………12分
综上,实数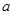 的取值范围为
的取值范围为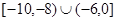 ……………………13分
……………………13分
考点: 复合命题的真假判断,函数的零点,函数的极值.
点评:复合命题真假判定方法:或命题是有真则真;且命题是有假则假,非命题是真假相反.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 是定义在
是定义在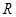 上的奇函数,且当
上的奇函数,且当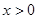 时,
时,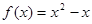 +1.
+1.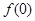 ,
,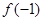 ; (2)当
; (2)当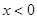 时,求
时,求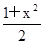 对一切实数x均成立?
对一切实数x均成立?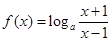 (
(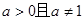 ).
).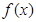 的奇偶性,并证明;
的奇偶性,并证明;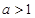 ,用单调性定义证明函数
,用单调性定义证明函数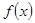 在区间
在区间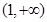 上单调递减;
上单调递减; ,使得
,使得 时,值域为
时,值域为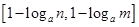 ,若存在,求出实数
,若存在,求出实数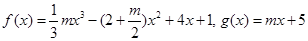 .
.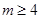 时,求
时,求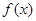 的单调递增区间;
的单调递增区间;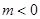 ,使得对任意的
,使得对任意的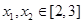 ,都有
,都有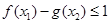 恒成立.若存在,求出
恒成立.若存在,求出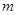 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.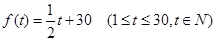 ,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN). ,函数
,函数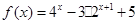 (其中
(其中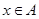 )
) 的定义域;
的定义域;