题目内容
(本小题满分12分)
已知函数 ,
,
(1) 若存在实数 ,使得
,使得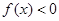 ,求实数
,求实数 的取值范围;
的取值范围;
(2) 设 ,且
,且 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
(1)存在实数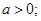 或
或 ;(2)
;(2) 。
。
解析试题分析:(1)直接零函数小于零,解一元二次不等式即可
(2)根据 ,且
,且 在区间
在区间 上单调递增,那么可知对于参数a进行分类讨论得到结论。
上单调递增,那么可知对于参数a进行分类讨论得到结论。
解:(1)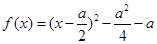 ,当仅当
,当仅当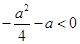 时,存在实数
时,存在实数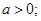 或
或 …………………3分
…………………3分
(2)当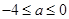 时,
时, 在
在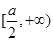 上递增,则
上递增,则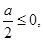 即
即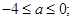 …………………5分
…………………5分
当 或
或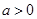 时,设
时,设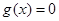 的两根为
的两根为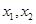 ,且
,且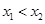 ,此时
,此时 在区间
在区间 或
或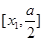 上递增。…………………7分。
上递增。…………………7分。
若 ,则
,则 ,得
,得 ;…………………9分
;…………………9分
若 ,则
,则 ,得
,得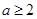 ,…………………11分
,…………………11分
综上可知, 的取值范围是
的取值范围是 …………………12分。
…………………12分。
考点:本试题主要考查了一元二次不等式的求解以及函数单调性的运用。
点评:解决该试题的关键是根据已知条件得到二次不等式,结合二次函数性质得到结论。同时对于绝对值函数,要分类去掉其符号。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
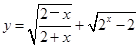 的定义域为
的定义域为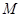 ,
, 时,求函数
时,求函数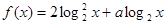 的最大值。
的最大值。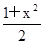 对一切实数x均成立?
对一切实数x均成立?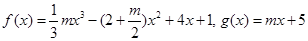 .
.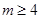 时,求
时,求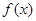 的单调递增区间;
的单调递增区间;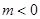 ,使得对任意的
,使得对任意的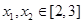 ,都有
,都有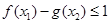 恒成立.若存在,求出
恒成立.若存在,求出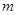 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.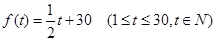 ,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN). ,函数
,函数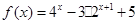 (其中
(其中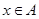 )
) 的定义域;
的定义域; .
. 的图像;
的图像; .
.
 的单调区间.
的单调区间.