题目内容
(本小题满分12分)某炮兵阵地位于地面A处,两观察所分别位于地面点C和D处, 已知CD=6000m,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.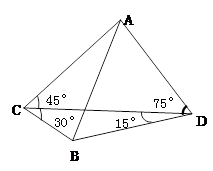
 .
.
解析试题分析:在△ACD中,依题意可求得,∠CAD,利用正弦定理求得BD的长,进而在△ABD中,利用勾股定理求得AB.
解:在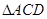 中,
中,
根据正弦定理有: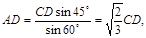
同理:在 中,
中,
 ,
,
根据正弦定理有: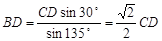 在
在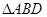 中,
中,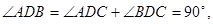 根据勾股定理有:
根据勾股定理有: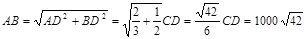
所以:炮兵阵地到目标的距离为 .………………………………12分
.………………………………12分
考点:本试题主要考查了解三角形的实际应用.利用了正弦定理和余弦整体定理,完成了边角的问题的互化.
点评:解决该试题的关键是在△ACD中,利用正弦定理求得BD的长,在△ABD中,利用勾股定理求得AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
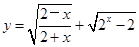 的定义域为
的定义域为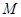 ,
,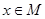 时,求函数
时,求函数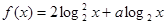 的最大值。
的最大值。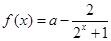 (其中常数
(其中常数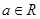 )
) 的单调性,并加以证明;
的单调性,并加以证明; 的值。
的值。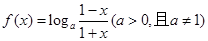
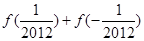 的值;
的值;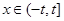 (其中
(其中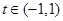 ,且
,且 为常数)时,
为常数)时,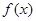 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如 时,求满足不等式
时,求满足不等式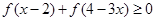 的
的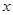 的范围.
的范围. 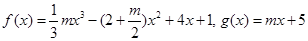 .
.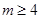 时,求
时,求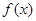 的单调递增区间;
的单调递增区间;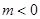 ,使得对任意的
,使得对任意的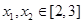 ,都有
,都有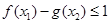 恒成立.若存在,求出
恒成立.若存在,求出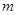 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.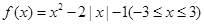
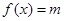 有两个根,试求
有两个根,试求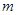 的取值范围。
的取值范围。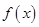 是定义在
是定义在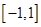 上的奇函数,且
上的奇函数,且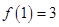 ,若
,若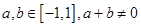 时,有
时,有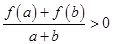 成立.
成立.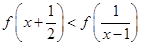 ;
;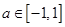 时,
时,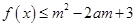 对所有的
对所有的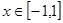 恒成立,求实数
恒成立,求实数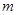 的取值范围.
的取值范围.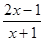 , x∈[3, 5]
, x∈[3, 5]