题目内容
2.若点(a,9)在函数$y={(\sqrt{3})^x}$的图象上,则${log_{\sqrt{2}}}$a=4.分析 利用指数与对数的运算法则即可得出.
解答 解:∵点(a,9)在函数$y={(\sqrt{3})^x}$的图象上,
∴$9=(\sqrt{3})^{a}$,∴${3}^{2}={3}^{\frac{a}{2}}$,解得a=4.
∴${log_{\sqrt{2}}}$a=$lo{g}_{\sqrt{2}}4$=$lo{g}_{\sqrt{2}}(\sqrt{2})^{4}$=4.
故答案为:4.
点评 本题考查了指数与对数的运算法则,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
13.已知等比数列{an}的前n项和为Sn,公比为q,若a3=2S2+1,a4=2S3+1,则q等于( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
10.已知x,y满足约束条件$\left\{\begin{array}{l}{x^2}+{y^2}≤4\\ x-2y-2≤0\\ 2x-y+2≥0\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | 4 | D. | $2\sqrt{5}$ |
11.在平面直角坐标系中,角α的顶点与原点重合,始边与x轴的非负半轴重合,终边过点P(-$\sqrt{3}$,-1),则sin(2α-$\frac{π}{2}$)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |

 如图:$\widehat{BCD}$是直径为2$\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,BF=2$\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.
如图:$\widehat{BCD}$是直径为2$\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,BF=2$\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.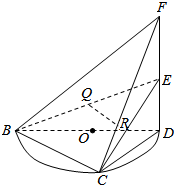 如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.
如图:$\widehat{BCD}$是直径为$2\sqrt{2}$的半圆,O为圆心,C是$\widehat{BD}$上一点,且$\widehat{BC}=2\widehat{CD}$.DF⊥CD,且DF=2,$BF=2\sqrt{3}$,E为FD的中点,Q为BE的中点,R为FC上一点,且FR=3RC.