题目内容
1.设向量$\overrightarrow m$=(sin2ωx,cos2ωx),$\overrightarrow n$=(cosφ,sinφ),其中|φ|<$\frac{π}{2}$,ω>0,函数f(x)=$\overrightarrow m•\overrightarrow n$的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为$P(\frac{π}{6},1)$,在原点右侧与x轴的第一个交点为$Q(\frac{5π}{12},0)$.(Ⅰ)求函数f(x)的表达式;
(Ⅱ)在△ABC中,角A′B′C的对边分别是a′b′c′若f(C)=-1,$\overrightarrow{CA}•\overrightarrow{CB}=-\frac{3}{2}$,且a+b=2$\sqrt{3}$,求边长c.
分析 (I)利用向量的数量积通过两角和与差的三角函数化简函数的解析式,利用已知条件求解解析式即可.
(II)求出C,利用$\overrightarrow{CA}•\overrightarrow{CB}=-\frac{3}{2}$,以及余弦定理即可求出c的值.
解答 解:(I)因为向量$\overrightarrow m$=(sin2ωx,cos2ωx),$\overrightarrow n$=(cosφ,sinφ),
所以$f(x)=\overrightarrow m•\overrightarrow n$=sin2ωxcosφ+cos2ωxsinφ=sin(2ωx+φ),----------------1分
由题意$\frac{T}{4}=\frac{5π}{12}-\frac{π}{6}∴T=π∴ω=1$,-----------------------------3分
将点$P(\frac{π}{6},1)$代入y=sin(2x+φ),得$sin(2×\frac{π}{6}+φ)=1$,
所以$φ=\frac{π}{6}+2kπ,(k∈{Z})$,又因为$|φ|<\frac{π}{2}$,∴$φ=\frac{π}{6}$-------------------5分
即函数的表达式为$f(x)=sin(2x+\frac{π}{6}),(x∈R)$.---------------------6分
(II)由f(C)=-1,即$sin(2C+\frac{π}{6})=-1$
又∵0<C<π,∴$C=\frac{2π}{3}$------------------------8分
由$\overrightarrow{CA}•\overrightarrow{CB}=-\frac{3}{2}$,知$abcosC=-\frac{3}{2}$,
所以ab=3-----------------10分
由余弦定理知c2=a2+b2-2abcosC=(a+b)2-2ab-2abcosC=${(2\sqrt{3})^2}-2×3-2×3×(-\frac{1}{2})=9$
所以 c=3----------------------------------------------------12分.
点评 本题考查余弦定理的应用,两角和与差的三角函数,三角形的解法,考查计算能力.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | (-∞,3] | B. | [2,3] | C. | (2,+∞) | D. | (2,3) |

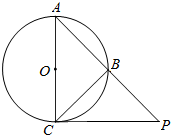 如图,已知AB是⊙O的一条弦,AC是⊙O的直径,点P为AB延长线上一点,且PC为⊙O的一条切线,若AO=$\sqrt{2}$,PB=2,则PC的长是$2\sqrt{2}$.
如图,已知AB是⊙O的一条弦,AC是⊙O的直径,点P为AB延长线上一点,且PC为⊙O的一条切线,若AO=$\sqrt{2}$,PB=2,则PC的长是$2\sqrt{2}$.