题目内容
19.求证:曲线y=$\frac{{a}^{2}}{x}$(a为非零常数)上任何一点处的切线与坐标轴围成的三角形的面积为定值.分析 求出函数的导数,求出切线的斜率,求出切线方程,求出x,y轴上的截距,运用三角形的面积公式,即可得证.
解答 证明:曲线y=$\frac{{a}^{2}}{x}$的导数为y′=-$\frac{{a}^{2}}{{x}^{2}}$,
在任一点(x0,y0)处的切线斜率为-$\frac{{a}^{2}}{{{x}_{0}}^{2}}$,
切点为(x0,$\frac{{a}^{2}}{{x}_{0}}$),
则有切线方程:y-$\frac{{a}^{2}}{{x}_{0}}$=-$\frac{{a}^{2}}{{{x}_{0}}^{2}}$(x-x0),
由x=0得,y=$\frac{2{a}^{2}}{{x}_{0}}$,
再由y=0,得,x=2x0,
则与两坐标轴围成的三角形面积是:$\frac{1}{2}$|2x0•$\frac{2{a}^{2}}{{x}_{0}}$|=2a2为定值.
点评 本题考查导数的运用:求切线方程,考查直线方程的点斜式,考查运算能力,属于基础题.

练习册系列答案
相关题目
9.集合{y∈Z|1<y≤5}的子集个数是( )
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
10.f(x)=$\frac{lnx}{x}$的极大值是( )
| A. | e | B. | $\frac{1}{e}$ | C. | -e | D. | -$\frac{1}{e}$ |
7.设函数f(x)=log2$\frac{2{x}^{2}}{{x}^{2}+1}$(x>0),若函数g(x)=|f(x)|2+m|f(x)|+2m+3有三个零点,则实数m的最大值为( )
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
8.在△ABC中,若cosAcosB=-cos2$\frac{C}{2}$+1,则△ABC一定是( )
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
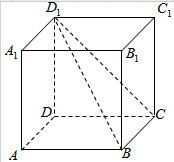 如图,在正方体ABCD-A1B1C1D1中,找出二面角D1-BC-D的平面角.
如图,在正方体ABCD-A1B1C1D1中,找出二面角D1-BC-D的平面角.