题目内容
4.函数f(x)=e2x的图象上的点到直线2x-y-4=0的距离的最小值是$\sqrt{5}$.分析 由函数图象上到直线距离最小的点做函数图象的切线,与已知直线平行即斜率相等,先求出切点坐标,然后利用点到直线的距离公式解之即可.
解答 解:设与2x-y-4=0平行的切线横坐标为a,则切线斜率k=y′=2e2a,
而已知直线的斜率为2,
所以2e2a=2,
解得a=0,
把a=0代入y=e2x中求得y=1,所以切点坐标是(0,1),
则函数图象上的点到直线距离的最小值d=$\frac{|-1-4|}{\sqrt{{2}^{2}+{(-1)}^{2}}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及点到直线的距离公式的应用,同时考查了导数的几何意义,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
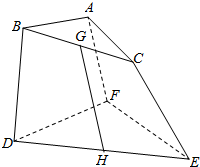 如图,BD=CE,G、H为BC、DE中点,AB=AC,FD=FE,∠BAC=∠DFE.求证:AF∥GH.
如图,BD=CE,G、H为BC、DE中点,AB=AC,FD=FE,∠BAC=∠DFE.求证:AF∥GH.