题目内容
10.f(x)=$\frac{lnx}{x}$的极大值是( )| A. | e | B. | $\frac{1}{e}$ | C. | -e | D. | -$\frac{1}{e}$ |
分析 求出函数的导数,利用函数的极值点,判断即可.
解答 解:f(x)=$\frac{lnx}{x}$,可得f′(x)=$\frac{1-lnx}{{x}^{2}}$,
令$\frac{1-lnx}{{x}^{2}}$=0,可得x=e,
当x∈(0,1)时,f′(x)>0,x∈(e,+∞)时,f′(x)<0,
可得x=e时,函数取得极大值.
函数的最大值为:$\frac{lne}{e}$=$\frac{1}{e}$.
故选:B.
点评 本题考查函数的极值的判断与求解,考查计算能力.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
18.如图,函数y=f(x)的图象在点P(2,y)处的切线是L,则f(2)+f′(2)=( )


| A. | -4 | B. | 3 | C. | -2 | D. | 1 |
2.甲乙两人向某个目标射击,他们每次击中目标的概率如下表:
(Ⅰ)若两人同时向目标射击一次,求目标被击中的概率;
(Ⅱ)若由甲开始两人轮流向目标射击,击中目标就停止,现在共有5发子弹,写出使用子弹数?分布列,求?的期望(均值).
| 第一次 | 第二次 | 第三次 | |
| 甲 | 0.4 | 0.6 | 0.8 |
| 乙 | 0.5 | 0.6 | 0.9 |
(Ⅱ)若由甲开始两人轮流向目标射击,击中目标就停止,现在共有5发子弹,写出使用子弹数?分布列,求?的期望(均值).
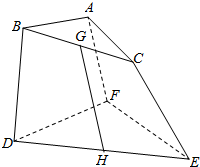 如图,BD=CE,G、H为BC、DE中点,AB=AC,FD=FE,∠BAC=∠DFE.求证:AF∥GH.
如图,BD=CE,G、H为BC、DE中点,AB=AC,FD=FE,∠BAC=∠DFE.求证:AF∥GH.