题目内容
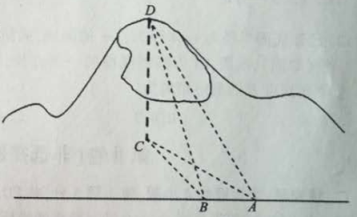
【题目】如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=![]() .
.
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求二面角O﹣AC﹣D的大小.

【答案】(1)证明过程详见解析(2)![]() (3)
(3)![]()
【解析】
(1)设![]() 是
是![]() 的中点,由等腰三角形的性质可得
的中点,由等腰三角形的性质可得![]() ,根据勾股定理可证明
,根据勾股定理可证明![]() ,从而证明
,从而证明![]() 平面
平面![]() ;(2)利用公式
;(2)利用公式![]()
![]() ,直接求异面直线
,直接求异面直线![]() 与
与![]() 所成角的的余弦值,然后求出角的大小;(3)利用射影面的面积与被射影面的面积的比,求二面角
所成角的的余弦值,然后求出角的大小;(3)利用射影面的面积与被射影面的面积的比,求二面角![]() 的余弦值,从而可得二面角的大小.
的余弦值,从而可得二面角的大小.
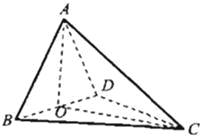
(1)设O是等腰直角三角形ABD斜边BD的中点,
所以有AO⊥BD,可求得AO=1,CO=![]() ,又有AC=2
,又有AC=2
所以∠AOC=90°,即AO⊥CO
BD,CO是平面BCD内两条相交直线,故有AO⊥平面BCD.
(2)由(1)可知BD⊥面AOC,
所以面BCD⊥面AOC,AO=1,CO=![]() ,AC=2
,AC=2
A点在BCD面内的投影为O,
cos<AB,CD>=cos∠ABDcos∠BDC=![]() =
=![]()
异面直线AB与CD所成角的大小为:arccos![]() .
.
(3)三角形AOC的面积为:![]() =
=![]() ;三角形ADC的面积为:
;三角形ADC的面积为:![]() =
=![]() ;
;
所以二面角O﹣AC﹣D的余弦为: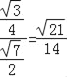 ,
,
二面角O﹣AC﹣D的大小为:arccos![]() .
.

练习册系列答案
相关题目