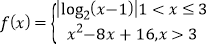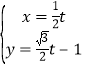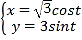题目内容
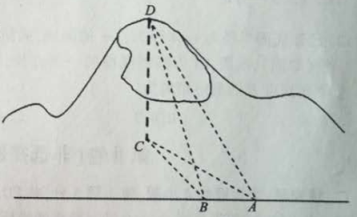
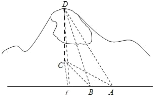
【题目】如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北![]() 的方向上,仰角为
的方向上,仰角为![]() ,行驶4km后到达B处,测得此山顶在西偏北
,行驶4km后到达B处,测得此山顶在西偏北![]() 的方向上.
的方向上.
(1)求此山的高度(单位:km);
(2)设汽车行驶过程中仰望山顶D的最大仰角为![]() ,求
,求![]() .
.
【答案】(1)![]() km.(2)
km.(2)![]()
【解析】
(1) 设此山高![]() ,再根据三角形中三角函数的关系以及正弦定理求解即可.
,再根据三角形中三角函数的关系以及正弦定理求解即可.
(2) 由题意可知,当点C到公路距离最小时,仰望山顶D的仰角达到最大,再计算![]() 到直线
到直线![]() 的距离即可.
的距离即可.
解:(1)设此山高![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
根据正弦定理得![]() ,
,
即![]() ,
,
解得![]() (km).
(km).
(2)由题意可知,当点C到公路距离最小时,仰望山顶D的仰角达到最大,
所以过C作![]() ,垂足为E,连接DE.
,垂足为E,连接DE.
则![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
【题目】某校高一年级新入学360名学生,其中200名男生,160名女生.学校计划为家远的高一新生提供5间男生宿舍和4间女生宿舍,每间宿舍可住2名学生.该校“数学与统计”社团的学生为了解全体高一学生家庭居住地与学校的距离情况,按照性别进行分层随机抽样,其中抽取的40名男生家庭居住地与学校的距离数据(单位:![]() )如下:
)如下:
5.0 | 6.0 | 7.0 | 7.5 | 8.0 | 8.4 | 4.0 | 3.5 | 4.5 |
4.3 | 5.0 | 4.0 | 3.0 | 2.5 | 4.0 | 1.6 | 6.0 | 6.5 |
5.5 | 5.7 | 3.1 | 5.2 | 4.4 | 5.0 | 6.4 | 3.5 | 7.0 |
4.0 | 3.0 | 3.4 | 6.9 | 4.8 | 5.6 | 5.0 | 5.6 | 6.5 |
3.0 | 6.0 | 7.0 | 6.6 |
(1)根据以上样本数据推断,若男生甲家庭居中地与学校距离为![]() ,他是否能住宿?说明理由;
,他是否能住宿?说明理由;
(2)通过计算得到男生样本数据平均值为![]() ,女生样本数据平均值为
,女生样本数据平均值为![]() ,求所有样本数据的平均值.
,求所有样本数据的平均值.