题目内容
已知:以点C(t, )(t∈R,t≠0)为圆心的圆与
)(t∈R,t≠0)为圆心的圆与 轴交于点O,A,与y轴交于点O,B,其中O为原点
轴交于点O,A,与y轴交于点O,B,其中O为原点
(1)求证:△OAB的面积为定值;
(2)设直线y=–2x+4与圆C交于点M,N,若OM=ON,求圆C的方程
(1)参考解析;(2)
解析试题分析:(1)因为要证△OAB的面积为定值,关键是要求出A,B两点的坐标 根据圆的半径是 即
即 所以可以写出圆C的方程 从而分别令
所以可以写出圆C的方程 从而分别令 即可求得A,B两点的坐标 再根据
即可求得A,B两点的坐标 再根据 就即可证得结论
就即可证得结论
(2)因为直线y=–2x+4与圆C交于点M,N,若OM="ON" 又因为 所以可得
所以可得 由直线
由直线 的斜率即可求得直线
的斜率即可求得直线 的斜率,从而得到直线
的斜率,从而得到直线 的方程,在代入C (t,
的方程,在代入C (t, ) 即可求得
) 即可求得 的值,再根据
的值,再根据 的值判断直线与圆的关系 从而确定圆的方程
的值判断直线与圆的关系 从而确定圆的方程
试题解析:(1)因为圆C过原点O,
设圆 的方程是
的方程是  令
令 得
得 ;令
;令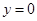 得
得 所以
所以 ,即
,即 的面积为定值
的面积为定值
(2)因为 垂直平分线段
垂直平分线段 因为
因为 ,所以直线
,所以直线 的方程是
的方程是 所以
所以 ,解得
,解得 或
或 当
当 时,圆心
时,圆心 的坐标为
的坐标为
此时 到直线
到直线 的距离
的距离 ,
,
圆 与直线
与直线 相交于两点 10分
相交于两点 10分
当 时,圆心
时,圆心 的坐标为
的坐标为 ,
, ,
,
此时 到直线
到直线 的距离
的距离
圆 与直线
与直线 不相交,
不相交, 不符合题意舍去 11分
不符合题意舍去 11分 圆
圆 的方程为
的方程为 13分
13分
考点:1 圆的方程 2 直线与圆的方程 3 圆的对称性

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的方程为
的方程为 ,点
,点 是坐标原点.直线
是坐标原点.直线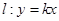 与圆
与圆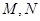 两点.
两点. 的取值范围;
的取值范围; 作圆的弦,求最小弦长?
作圆的弦,求最小弦长?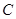 经过坐标原点
经过坐标原点 和点
和点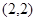 ,且圆心在
,且圆心在 轴上.
轴上.  经过点
经过点 ,且
,且 ,求直线
,求直线 ,圆心在直线
,圆心在直线 :
: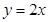 上,且被直线
上,且被直线 :
: 所截弦的长为
所截弦的长为 的圆的方程.
的圆的方程.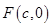 是椭圆
是椭圆 的右焦点;圆
的右焦点;圆 与
与 轴交于
轴交于 两点,其中
两点,其中 是椭圆
是椭圆 的左焦点.
的左焦点.
 与
与 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点 关于
关于 与圆
与圆 与圆
与圆 ,若
,若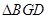 的面积为
的面积为 ,求椭圆
,求椭圆 关于直线
关于直线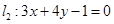 ,对称的直线方程;
,对称的直线方程;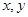 满足
满足 ,求
,求 的取值范围.
的取值范围. 中,已知圆
中,已知圆 :
: 和直线
和直线 :
: ,
, 为
为 ,
, 为圆
为圆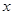 轴的两个交点,直线
轴的两个交点,直线 ,
, 与圆
与圆 .
. 方程;
方程; 是圆
是圆 上的点
上的点 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.