题目内容
已知圆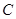 经过坐标原点
经过坐标原点 和点
和点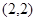 ,且圆心在
,且圆心在 轴上.
轴上.
(1)求圆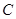 的方程;
的方程;
(2)设直线 经过点
经过点 ,且
,且 与圆
与圆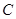 相交所得弦长为
相交所得弦长为 ,求直线
,求直线 的方程.
的方程.
(1)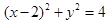 ;(2)
;(2)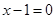 或
或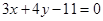
解析试题分析:(1)本题求圆的方程,已知圆上两点即圆心的纵坐标,所以需要求出圆的半径和圆心的横坐标两个值即可确定圆的方程,通过列解方程即可求出相应的量,该题的半径的长刚好就是圆心的横坐标的值,这个条件要用上.
(2)该小题是直线与圆的位置关系问题,特别要先判断直线的斜率不存在的时候的情况,通过画图可知符合条件,其次是斜率存在时,通过重点三角形(弦心距,半弦长,半径)的关系可以求出弦心距的长,从而再用圆心到直线的距离公式求出直线的斜率,又过已知点即可写出直线方程.
试题解析:(1)设圆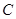 的圆心坐标为
的圆心坐标为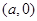 ,
,
依题意,有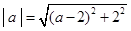 ,
,
即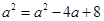 ,解得
,解得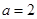 ,所以圆
,所以圆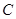 的方程为
的方程为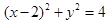 .
.
(2)依题意,圆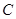 的圆心到直线
的圆心到直线 的距离为
的距离为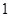 ,
,
所以直线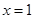 符合题意.
符合题意.
另,设直线 方程为
方程为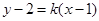 ,即
,即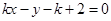 ,
,
则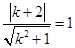 ,
,
解得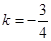 ,
,
所以直线 的方程为
的方程为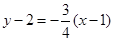 ,即
,即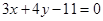 .
.
综上,直线 的方程为
的方程为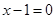 或
或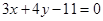 .
.
考点:1.直线与圆的关系.2.圆的标准方程.3.分类归纳思想.4.运算能力的锻炼.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目

 的方程为
的方程为 ,直线
,直线 的方程为
的方程为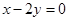 ,点
,点 在直线
在直线 ,切点为
,切点为 .
. ,试求点
,试求点 点的坐标为
点的坐标为 ,过
,过 两点,当
两点,当 时,求直线
时,求直线 的方程;
的方程; ,
, )的直线
)的直线 与圆
与圆 相切,求直线
相切,求直线 )且倾斜角为
)且倾斜角为 的直线
的直线 两点,求线段
两点,求线段 的中点
的中点 的坐标;
的坐标; 的直线
的直线 ,且以
,且以 的圆与直线
的圆与直线 相切.
相切.
 的标准方程;
的标准方程; ,是否存在定点
,是否存在定点 (不同于原点
(不同于原点 )使得
)使得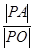 恒为常数?若存在,求出点
恒为常数?若存在,求出点 )(t∈R,t≠0)为圆心的圆与
)(t∈R,t≠0)为圆心的圆与 轴交于点O,A,与y轴交于点O,B,其中O为原点
轴交于点O,A,与y轴交于点O,B,其中O为原点  ,点
,点 .
.
 上,经过点
上,经过点 ,且与圆
,且与圆 相外切的圆
相外切的圆 的方程;
的方程; 与圆
与圆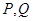 两点,且圆弧
两点,且圆弧 恰为圆
恰为圆 ,求直线
,求直线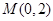 ,
, ,直线
,直线 (
( 为常数).
为常数).  、
、 到直线
到直线 的距离相等,求实数
的距离相等,求实数 ,
,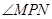 恒为锐角,求实数
恒为锐角,求实数