[题目]已知椭圆的两焦点分别为.其短半轴长为.(1)求椭圆的方程,(2)设不经过点的直线与椭圆相交于两点.若直线与的斜率之和为.求实数的值. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆的两焦点分别为，其短半轴长为.

（1）求椭圆的方程；

（2）设不经过点的直线与椭圆相交于两点.若直线与的斜率之和为，求实数的值.

【答案】(1) ；(2)3.

【解析】

（1）根据题干条件得到a,b,c进而得到椭圆方程；（2）联立直线和椭圆方程得到二次方程，kHM+kHN，代入韦达定理,整理可得到结果.

（1）椭圆的两焦点分别为，c=, 短半轴长为,b=1, ,故得到曲线C的方程为：；

（2）设M（x1，y1），N（x2，y2），

由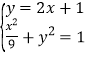，消去y得，

37x2+36tx+9（t2﹣1）＝0，

由△＝（36t）2﹣4×37×9（t2﹣1）＞0，

可得﹣，

又直线y＝2x+t不经过点H（0，1），

且直线HM与HN的斜率存在，

∴t≠±1，

又，，

∴kHM+kHN＝，

解得t＝3，

故t的值为3.

练习册系列答案

相关题目

【题目】已知称为，的二维平方平均数，称为，的二维算术平均数，称为，的二维几何平均数，称为，的二维调和平均数，其中，均为正数.

（1）试判断与的大小，并证明你的猜想.

（2）令，，试判断与的大小，并证明你的猜想.

（3）令，，，试判断、、三者之间的大小关系，并证明你的猜想.

【题目】如图，已知椭圆的中心在原点，焦点在轴上，长轴长是短轴长的2倍且经过点，平行于的直线在轴上的截距为，直线交椭圆于两个不同点．

（1）求椭圆的方程；

（2）求的取值范围．

【题目】已知△ABC的顶点C在直线3x﹣y=0上，顶点A、B的坐标分别为（4，2），（0，5）．

（Ⅰ）求过点A且在x，y轴上的截距相等的直线方程；

（Ⅱ）若△ABC的面积为10，求顶点C的坐标．

【题目】如图所示，合肥一中积极开展美丽校园建设，现拟在边长为0.6千米的正方形地块上划出一片三角形地块建设小型生态园，点分别在边上.

（1）当点分别时边中点和靠近的三等分点时，求的余弦值；

（2）实地勘察后发现，由于地形等原因，的周长必须为1.2千米，请研究是否为定值，若是，求此定值，若不是，请说明理由.

【题目】2018年2月25日，平昌冬奥会闭幕式上的“北京8分钟”惊艳了世界。我们学校为了让我们更好的了解奥运，了解新时代祖国的科技发展，在高二年级举办了一次知识问答比赛。比赛共设三关，第一、二关各有两个问题，两个问题全答对，可进入下一关；第三关有三个问题，只要答对其中两个问题，则闯关成功。每过一关可一次性获得分别为1、2、3分的积分奖励，高二、一班对三关中每个问题回答正确的概率依次为，且每个问题回答正确与否相互独立.