Question

【题目】已知函数f（x）＝cos2x+2sinxcosx﹣sin2x．

（1）求函数f（x）的最小正周期

（2）求函数f（x）单调增区间．

Answer 1

【答案】（1）Tπ；（2）[kπ，kπ]，k∈Z．

【解析】

（1）利用辅助角二倍角公式化简，即可求函数f（x）的最小正周期

（2）根据三角函数的性质即可求出函数f（x）单调增区间．

函数f（x）＝cos2x+2sinxcosx﹣sin2x．

化简可得：f（x）＝cos2x﹣sin2x+2sinxcosx

＝cos2xsin2x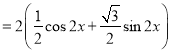

＝2sin（2x），

（1）∵ω＝2，

∴f（x）的最小正周期为Tπ；

（2）令2kπ2x2kπ（k∈Z），

解得：kπx≤π，k∈Z，

则f（x）的单调增区间为[kπ，kπ]，k∈Z．