函数y=$\frac{x}{{x}^{2}+1}$的图象与函数y=sin$\frac{π}{2}$x的图象所有交点的横坐标之和等于( )A．0B．4C．10D．2π 题目和参考答案——青夏教育精英家教网—

题目内容

1．函数y=$\frac{x}{{x}^{2}+1}$的图象与函数y=sin$\frac{π}{2}$x（-5≤x≤5）的图象所有交点的横坐标之和等于（　　）

A．

B．

C．

D．

2π

分析先判断出两个函数都是奇函数，所对应的交点的坐标互为相反数，从而求出答案．

解答解：∵函数y=$\frac{x}{{x}^{2}+1}$和函数y=sin$\frac{π}{2}$x（-5≤x≤5）都是奇函数，
∴所有交点的横坐标之和等于0，
故选：A．

点评本题考查了函数的奇偶性，考查了函数的零点问题，是一道基础题．

练习册系列答案

相关题目

7．

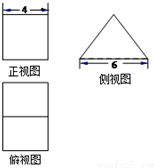一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形，则该几何体的表面积是（　　）

12．设函数f（x）=$\frac{\sqrt{2}}{2}$cos（2x+$\frac{π}{4}$）+sin²x
（1）求f（x）的最小正周期和单调增区间；
（2）设函数g（x）对任意x∈R，有$g（x+\frac{π}{2}）=g（x）$，且当$x∈[{0，\frac{π}{2}}]$时，g（x）=$\frac{1}{2}$-f（x），求g（x）在区间[-π，0]上的解析式．

9．若$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，-2），$\overrightarrow{c}$=（2，1），则（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=（-16，-8），$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$）=（-8，-12）．

16．若不等式（m-2）x²+2（m-2）x-4＜0的解集为R，求实数m的范围．

6．已知f（x）=2asinωxcosωx+2$\sqrt{3}{cos^2}ωx-\sqrt{3}（{a＞0，ω＞0}）$的最大值为2，且最小正周期为π．
（1）求函数f（x）的解析式及其对称轴方程；
（2）若$f（{α-\frac{π}{6}}）=\frac{4}{3}$，求cos4α的值．

13．校庆期间，某同学从2本相同的画册和3个相同的纪念章中，任取4件作为礼物赠送给4为校友，每人1件，则不同的赠送方法共有（　　）

10．已知：a=$\root{3}{4}$+$\root{3}{2}$+$\root{3}{1}$，那么$\frac{3}{a}$+$\frac{3}{{a}^{2}}$+$\frac{1}{{a}^{3}}$=1．

11．淘宝卖家在某商品的所有买家中，随机选择男女买家各50名进行调查，他们的评分等级如表：

评分等级	[0，1]	（1，2]	（2，3]	（3，4]	（4，5]
女（人数）	2	7	9	20	12
男（人数）	3	9	18	12	8

规定：评分等级在[0，3]内为不满意该商品，在（3，5]内为满意该商品．完成下列2×2列联表并帮助卖家判断：能否在犯错误的概率不超过0.05的前提下认为满意该商品与性别有关系？

	满意该商品	不满意该商品	总计
女	32	18	50
男	20	30	50
总计	52	48	100

参考数据：

P（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：K²=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

试题分类