若$\overrightarrow{a}$=(2.3).$\overrightarrow{b}$=.$\overrightarrow{c}$=(2.1).则($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=.$\overrightarrow{a}$($\overrightarrow{b}$•$\o 题目和参考答案——青夏教育精英家教网—

题目内容

9．若$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，-2），$\overrightarrow{c}$=（2，1），则（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=（-16，-8），$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$）=（-8，-12）．

分析利用平面向量的数量积和数乘的坐标运算解答．

解答解：$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，-2），$\overrightarrow{c}$=（2，1），则（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=-8（2，1）=（-16，-8），
$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$）=-4（2，3）=（-8，-12）；
故答案为：（-16，-8）；（-8，-12）．

点评本题考查了平面向量的数量积和数乘的坐标运算，注意运算法则的运用；属于基础题．

练习册系列答案

中考分类必备全国中考真题分类汇编系列答案

16．已知P为△ABC所在平面内一点，且满足$\overrightarrow{AP}$=$\frac{1}{5}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$，则△APB的面积与△APC的面积之比为（　　）

17．

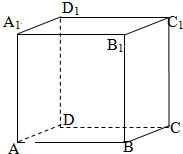ABCD-A₁B₁C₁D₁是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA₁→A₁D₁，…，黑蚂蚁爬行的路线是AB→BB₁，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N^*），设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（　　）

4．有两个不透明的箱子，每个箱子里都装有3个完全相同的小球，球上分别标有数字1，2，3．甲从其中一个箱子中随机摸出一个球，乙从另一个箱子中随机摸出一个球，谁摸出的球上标的数字大谁就获胜（若数字相同则为平局），则甲没有获胜的概率为$\frac{2}{3}$．

14．已知数列{a_n}的前n项和为S_n，且S_n=2ⁿ⁺¹-2，数列{b_n}满足b₁=1，b_n+1=b_n+2，n∈N^*．
（1）求数列{a_n}、{b_n}的通项公式；
（2）若c_n=a_nb_n，n∈N^*，求数列{c_n}的前n项和T_n．

1．函数y=$\frac{x}{{x}^{2}+1}$的图象与函数y=sin$\frac{π}{2}$x（-5≤x≤5）的图象所有交点的横坐标之和等于（　　）

18．数列{a_n}的前n项和为S_n，且满足a₁=1，2S_n=（n+1）a_n．
（1）求数列{a_n}的通项公式；
（2）求和T_n=$\frac{1}{{{a}_{2}}^{2}-1}$+$\frac{1}{{{a}_{3}}^{2}-1}$+$\frac{1}{{{a}_{4}}^{2}-1}$+…+$\frac{1}{{{a}_{n+1}}^{2}-1}$．

19．从装有4个红球和3个黑球的口袋内任取3个球，那么互斥而不对立的事件是（　　）

	A．	至少有一个红球与都是黑球		B．	至少有一个红球与恰有一个黑球
	C．	至少有一个红球与至少有一个黑球		D．	恰有一个红球与恰有两个红球

试题分类