题目内容
12.设函数f(x)=$\frac{\sqrt{2}}{2}$cos(2x+$\frac{π}{4}$)+sin2x(1)求f(x)的最小正周期和单调增区间;
(2)设函数g(x)对任意x∈R,有$g(x+\frac{π}{2})=g(x)$,且当$x∈[{0,\frac{π}{2}}]$时,g(x)=$\frac{1}{2}$-f(x),求g(x)在区间[-π,0]上的解析式.
分析 (1)利用两角和的余弦函数以及二倍角公式化简函数的表达式,直接利用周期公式求解即可.
(2)求出函数g(x)的周期,利用x∈[0,$\frac{π}{2}$]时,g(x)=$\frac{1}{2}$-f(x),对x分类求出函数的解析式即可.
解答 解:(1)∵f(x)=$\frac{\sqrt{2}}{2}$cos(2x+$\frac{π}{4}$)+sin2x
=$\frac{\sqrt{2}}{2}$($\frac{\sqrt{2}}{2}$cos2x-$\frac{\sqrt{2}}{2}$sin2x)+$\frac{1-cos2x}{2}$
=$\frac{1}{2}$-$\frac{1}{2}$sin2x.
∴f(x)的最小正周期T=$\frac{2π}{2}=π$,由2kπ+$\frac{π}{2}$≤2x≤2kπ+$\frac{3π}{2}$,k∈Z可得单调增区间为:[kπ$+\frac{π}{4}$,kπ+$\frac{3π}{4}$],k∈Z.
(2)当x∈[0,$\frac{π}{2}$]时g(x)=$\frac{1}{2}$-f(x)=$\frac{1}{2}$sin2x.
当x∈[-$\frac{π}{2}$,0]时,x+$\frac{π}{2}$∈[0,$\frac{π}{2}$],g(x)=g(x+$\frac{π}{2}$)=$\frac{1}{2}$sin2(x+$\frac{π}{2}$)=-$\frac{1}{2}$sin2x.
当x∈[-π,-$\frac{π}{2}$)时,x+π∈[0,$\frac{π}{2}$],g(x)=g(x+π)=$\frac{1}{2}$sin2(x+π)=$\frac{1}{2}$sin2x.
g(x)在区间[-π,0]上的解析式:g(x)=$\left\{\begin{array}{l}{-\frac{1}{2}sin2x}&{x∈[-\frac{π}{2},0]}\\{\frac{1}{2}sin2x}&{x∈[-π,-\frac{π}{2}]}\end{array}\right.$.
点评 本题考查三角函数中的恒等变换应用,三角函数的周期性及其求法,三角函数的化简,考查计算能力,属于基本知识的考查.

| A. | (x-2)2+(y+1)2=9 | B. | (x+2)2+(y-1)2=9 | C. | (x-2)2+(y+1)2=25 | D. | (x+2)2+(y-1)2=25 |
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<a<c |
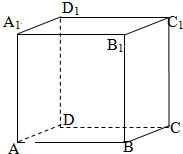 ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )
ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )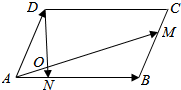 如图所示,□ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,BM=$\frac{2}{3}$BC,AN=$\frac{1}{4}$AB,
如图所示,□ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,BM=$\frac{2}{3}$BC,AN=$\frac{1}{4}$AB,