题目内容
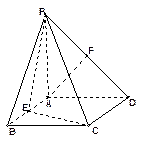
(本小题12分) 如图,四棱锥P-ABCD的底面是正方形, PA⊥底面ABCD, PA=2,
∠PDA="45°," 点E、F分别为棱AB、PD的中点.
(1)求证: AF∥平面PCE;
(2)求证: 平面PCE⊥平面PCD;
(3)求AF与平面PCB所成的角的大小.
∠PDA="45°," 点E、F分别为棱AB、PD的中点.

(1)求证: AF∥平面PCE;
(2)求证: 平面PCE⊥平面PCD;
(3)求AF与平面PCB所成的角的大小.
(1)证明见解析
(2)证明见解析
(3)30°
(2)证明见解析
(3)30°
证明: (1)取PC的中点G,连结FG、EG,

∴FG为△CDP的中位线 ∴FG CD
CD
∵四边形ABCD为矩形,E为AB的中点
∴AB CD ∴FG
CD ∴FG AE∴四边形AEGF是平行四边形∴AF∥EG
AE∴四边形AEGF是平行四边形∴AF∥EG
又EG 平面PCE,AF
平面PCE,AF 平面PCE∴AF∥平面PCE
平面PCE∴AF∥平面PCE
(2)∵PA⊥底面ABCD
∴PA⊥AD,PA⊥CD,又AD⊥CD,PA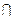 AD=A
AD=A
∴CD⊥平面ADP,又AF 平面ADP ∴CD⊥AF
平面ADP ∴CD⊥AF
直角三角形PAD中,∠PDA=45°
∴△PAD为等腰直角三角形 ∴PA=AD="2 "
∵F是PD的中点,∴AF⊥PD,又CD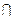 PD=D
PD=D
∴AF⊥平面PCD ∵AF∥EG ∴EG⊥平面PCD
又EG 平面PCE平面PCE⊥平面PCD
平面PCE平面PCE⊥平面PCD
(3)过E作EQ⊥PB于Q点, 连QG, CB⊥面PAB
∴
 QE⊥面PCB, 则∠QGE为所求的角.
QE⊥面PCB, 则∠QGE为所求的角.
S△PEB= BE·PA=
BE·PA= PB·EQ
PB·EQ EQ=
EQ=
在△PEC中, PE=EC= , G为PC的中点, ∴EG=
, G为PC的中点, ∴EG=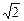 ,
,
在Rt△EGQ中, sin∠EGQ=
∴∠EGQ=30°

∴FG为△CDP的中位线 ∴FG
 CD
CD∵四边形ABCD为矩形,E为AB的中点
∴AB
 CD ∴FG
CD ∴FG AE∴四边形AEGF是平行四边形∴AF∥EG
AE∴四边形AEGF是平行四边形∴AF∥EG 又EG
 平面PCE,AF
平面PCE,AF 平面PCE∴AF∥平面PCE
平面PCE∴AF∥平面PCE (2)∵PA⊥底面ABCD
∴PA⊥AD,PA⊥CD,又AD⊥CD,PA
 AD=A
AD=A∴CD⊥平面ADP,又AF
 平面ADP ∴CD⊥AF
平面ADP ∴CD⊥AF直角三角形PAD中,∠PDA=45°
∴△PAD为等腰直角三角形 ∴PA=AD="2 "
∵F是PD的中点,∴AF⊥PD,又CD
 PD=D
PD=D∴AF⊥平面PCD ∵AF∥EG ∴EG⊥平面PCD
又EG
 平面PCE平面PCE⊥平面PCD
平面PCE平面PCE⊥平面PCD(3)过E作EQ⊥PB于Q点, 连QG, CB⊥面PAB
∴

 QE⊥面PCB, 则∠QGE为所求的角.
QE⊥面PCB, 则∠QGE为所求的角.S△PEB=
 BE·PA=
BE·PA= PB·EQ
PB·EQ EQ=
EQ=
在△PEC中, PE=EC=
 , G为PC的中点, ∴EG=
, G为PC的中点, ∴EG=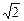 ,
,在Rt△EGQ中, sin∠EGQ=

∴∠EGQ=30°

练习册系列答案
相关题目
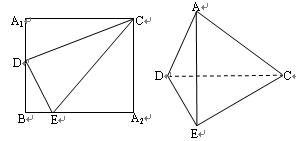
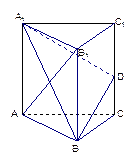
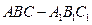 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由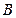 沿棱柱侧面经过棱
沿棱柱侧面经过棱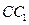 到点
到点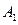 的最短路线长为
的最短路线长为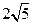 ,设这条最短路线与
,设这条最短路线与 .
.
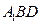 内是否存在过
内是否存在过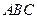 平行?证明你的判断;
平行?证明你的判断;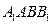 .
.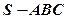 的底面边长为
的底面边长为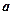 ,侧棱长为
,侧棱长为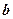 ,那么经过底边
,那么经过底边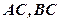 的中点且平行于侧棱
的中点且平行于侧棱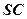 的截面面积为( )
的截面面积为( )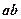
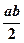
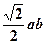
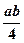
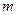 、
、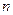 ,平面
,平面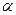 、
、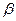 ,给出下列命题:
,给出下列命题:
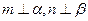 ,且
,且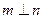 ,则
,则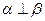 ②若
②若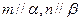 ,且
,且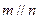 ,则
,则
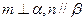 ,且
,且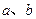 ,高为
,高为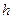 ,且侧面积等于两底面积之和,则下列关系正确的是
,且侧面积等于两底面积之和,则下列关系正确的是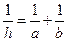
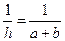
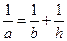
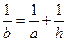
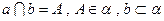
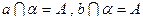
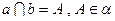
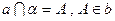
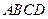 的顶点
的顶点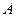 ,
,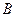 ,
,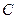 分别在两两垂直的三条射线
分别在两两垂直的三条射线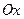 ,
,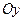 ,
,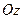 上,则在下列命题中,正确命题的个数为_______.
上,则在下列命题中,正确命题的个数为_______.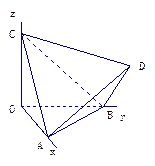
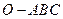 是正三棱锥 ;
是正三棱锥 ;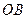 ∥平面
∥平面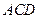 ;
;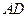 与
与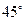 ;
; 为
为