题目内容
已知f(x)= ,则函数f(x)的零点个数为( )
,则函数f(x)的零点个数为( )
 ,则函数f(x)的零点个数为( )
,则函数f(x)的零点个数为( )| A.1 | B.2 | C.3 | D.4 |
B
当x>0时,由f(x)=0,即ln(x2-x+1)=0,得x2-x+1=1,解得x=0(舍去)或x=1.
当x≤0时,f(x)=ex-x-2,f′(x)=ex-1≤0,所以函数f(x)在(-∞,0]上单调递减.而f(0)=e0-0-2=-1<0,f(-2)=e-2-(-2)-2=e-2>0,故函数f(x)在(-2,0)上有且只有一个零点.
综上,函数f(x)只有两个零点.
当x≤0时,f(x)=ex-x-2,f′(x)=ex-1≤0,所以函数f(x)在(-∞,0]上单调递减.而f(0)=e0-0-2=-1<0,f(-2)=e-2-(-2)-2=e-2>0,故函数f(x)在(-2,0)上有且只有一个零点.
综上,函数f(x)只有两个零点.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
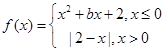 ,
,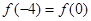 ,则函数
,则函数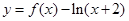 的零点有
的零点有 个.
个. (x>0).
(x>0). -
- (a>0)没有零点,则实数a的取值范围为________.
(a>0)没有零点,则实数a的取值范围为________.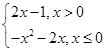 若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________.
若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________.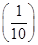 x在x∈[0,4]上解的个数是________.
x在x∈[0,4]上解的个数是________.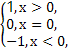 则函数f(x)=sgn(lnx)-lnx的零点个数为( )
则函数f(x)=sgn(lnx)-lnx的零点个数为( )