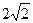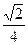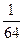题目内容
幂函数f(x)与g(x)分别过点(3,
)、(-8,-2)
(1)求此两个函数的解析式;
(2)判断两个函数的奇偶性;
(3)求函数f(x)<g(x)的解集.
| 4 | 27 |
(1)求此两个函数的解析式;
(2)判断两个函数的奇偶性;
(3)求函数f(x)<g(x)的解集.
(1)设幂函数f(x)=xa与g(x)=xb;
幂函数f(x)与g(x)分别过点(3,
)、(-8,-2)
所以:
=3a,-2=(-8)b;
∴a=
,b=
∴两个函数的解析式:f(x)=x
与g(x)=x
;
(2)f(x)=x
的定义域是x≥0,
所以它是非奇非偶函数;g(x)=x
因为g(-x)=-g(x),
所以是奇函数;
(3)因为函数f(x)<g(x),所以x
<x
(x≥0)
当1>x>0时,x
<x
成立;
当x>1时,x
<x
不成立;
所以不等式的解集为:{x|1>x>0}
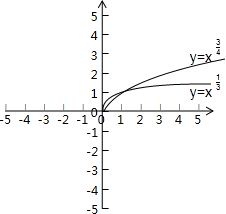
幂函数f(x)与g(x)分别过点(3,
| 4 | 27 |
所以:
| 4 | 27 |
∴a=
| 3 |
| 4 |
| 1 |
| 3 |
∴两个函数的解析式:f(x)=x
| 3 |
| 4 |
| 1 |
| 3 |
(2)f(x)=x
| 3 |
| 4 |
所以它是非奇非偶函数;g(x)=x
| 1 |
| 3 |
所以是奇函数;
(3)因为函数f(x)<g(x),所以x
| 3 |
| 4 |
| 1 |
| 3 |
当1>x>0时,x
| 3 |
| 4 |
| 1 |
| 3 |
当x>1时,x
| 3 |
| 4 |
| 1 |
| 3 |
所以不等式的解集为:{x|1>x>0}


练习册系列答案
相关题目
 ,T2=
,T2= ,T3=
,T3= ,则下列关系式正确的是( )
,则下列关系式正确的是( )
 的零点所在的一个区间是( ).
的零点所在的一个区间是( ). ,则函数f(x)的零点个数为( )
,则函数f(x)的零点个数为( )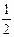 四个值,则相应于曲线
四个值,则相应于曲线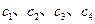 的n依次为( )
的n依次为( )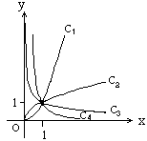
 的零点所在的大致区间是( )
的零点所在的大致区间是( ) )和(3, 4)
)和(3, 4)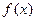 的图象过点
的图象过点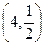 ,那么
,那么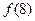 的值为 ( )
的值为 ( )