题目内容
【题目】已知两直线方程![]() 与
与![]() ,点
,点![]() 在
在![]() 上运动,点
上运动,点![]() 在
在![]() 上运动,且线段
上运动,且线段![]() 的长为定值
的长为定值![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求原点
,求原点![]() 的直线
的直线![]() 的距离的取值范围.
的距离的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)利用已知条件设![]() ,
,![]() ,
,![]() ,建立
,建立![]() 与
与![]() 的关系,利用线段
的关系,利用线段![]() 的长化简计算即可;
的长化简计算即可;
(Ⅱ)联立直线方程与椭圆方程,化为关于x的一元二次方程,由判别式大于0求得m2<4k2+1,再由![]() ,可得
,可得![]() ,从而求得k的范围,再由点到直线的距离公式求出原点O到直线l的距离,则取值范围可求.
,从而求得k的范围,再由点到直线的距离公式求出原点O到直线l的距离,则取值范围可求.
(Ⅰ)∵点![]() 在
在![]() 上运动,点
上运动,点![]() 在
在![]() 上运动,
上运动,
∴设![]() ,
,![]() ,线段
,线段![]() 的中点
的中点![]() ,则有
,则有![]() ,
,
∴![]() ,
,
∵线段![]() 的长为定值
的长为定值![]() ,∴
,∴![]() +
+![]() =8,
=8,
即![]() +
+![]() =8,化简得
=8,化简得![]() .
.
∴线段![]() 的中点
的中点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,联立
,联立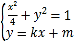 得
得![]()
![]() ,
,
![]()
![]() ,化简得
,化简得![]() ①.
①.
![]() ,
,![]()
![]()
![]() ,
,
若![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]()
![]() ,
,
即![]()
![]() ,化简得
,化简得![]() ②,
②,
由①②得![]() ,
,![]() ,
,
因为![]() 到直线
到直线![]() 的距离
的距离![]() ,所以
,所以![]()
![]()
又因为![]() ,所以
,所以![]() ,
,
所以![]() 到直线
到直线![]() 的距离的取值范围是
的距离的取值范围是![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目