题目内容
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
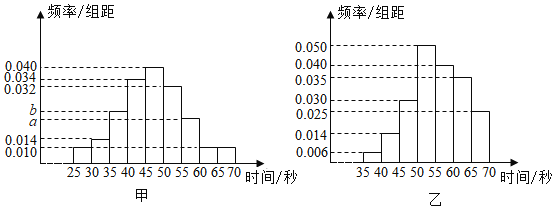
(1)若甲解开密码锁所需时间的中位数为47,求a、b的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①求该团队能进入下一关的概率;
②该团队以怎样的先后顺序派出人员,可使所需派出的人员数目X的数学期望达到最小,并说明理由.
【答案】(1)![]() ,
,![]() ,甲、乙在1分钟内解开密码锁的频率分别是0.9,0.7;(2)①0.985;②先派出甲,再派乙,最后派丙.
,甲、乙在1分钟内解开密码锁的频率分别是0.9,0.7;(2)①0.985;②先派出甲,再派乙,最后派丙.
【解析】
(1)根据频率分布直方图中左右两边矩形面积均为![]() 计算出中位数,可得出
计算出中位数,可得出![]() 、
、![]() 的值,再分别计算甲、乙在
的值,再分别计算甲、乙在![]() 分钟内解开密码锁的频率值;
分钟内解开密码锁的频率值;
(2)①利用独立事件概率的乘法公式可计算出所求事件的概率;
②分别求出先派甲和先派乙时随机变量![]() 的数学期望,比较它们的大小,即可得出结论。
的数学期望,比较它们的大小,即可得出结论。
(1)甲解开密码锁所需时间的中位数为47,
![]() ,解得
,解得![]() ;
;
![]() ,解得
,解得![]() ;
;
∴甲在1分钟内解开密码锁的频率是![]() ;
;
乙在1分钟内解开密码锁的频率是![]() ;
;
(2)由(1)知,甲在1分钟内解开密码锁的频率是0.9,乙是0.7,丙是0.5,
且各人是否解开密码锁相互独立;
①令“团队能进入下一关”的事件为![]() ,“不能进入下一关”的事件为
,“不能进入下一关”的事件为![]() ,
,
![]() ,
,
∴该团队能进入下一关的概率为![]() ;
;
②设甲、乙、丙三个人各自能完成任务的概率分别p1,p2,p3,且p1,p2,p3互不相等,
根据题意知X的取值为1,2,3;
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
若交换前两个人的派出顺序,则变为![]() ,
,
由此可见,当![]() 时,
时,
交换前两人的派出顺序可增大均值,应选概率大的甲先开锁;
若保持第一人派出的人选不变,交换后两人的派出顺序,
![]() ,
,
∴交换后的派出顺序则变为![]() ,
,
当![]() 时,交换后的派出顺序可增大均值;
时,交换后的派出顺序可增大均值;
所以先派出甲,再派乙,最后派丙,
这样能使所需派出的人员数目的均值(数学期望)达到最小.

【题目】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付,某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图:
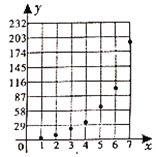
(I)根据散点图判断在推广期内,![]() 与
与![]() (c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(I)的判断结果求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.
参考数据:
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: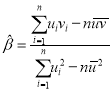 ,
,![]() 。
。