Question

【题目】已知极点为直角坐标系的原点，极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1：ρ=1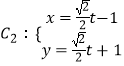， （t为参数）．
（Ⅰ）求曲线C1上的点到曲线C2距离的最小值；
（Ⅱ）若把C1上各点的横坐标都扩大为原来的2倍，纵坐标扩大为原来的 倍，得到曲线 ．设P（﹣1，1），曲线C2与 交于A，B两点，求|PA|+|PB|．

Answer 1

【答案】解：（Ⅰ）∵曲线C1：ρ=1，∴曲线C1的直角坐标方程为：x2+y2=1， ∴圆心为（0，0），半径为r=1，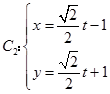
（t为参数）消去参数t的C2：y=x+2，
∴圆心到直线距离d= ，（3分）
∴曲线C1上的点到曲线C2距离的最小值为 ．
（Ⅱ）∵把C1上各点的横坐标都扩大为原来的2倍，纵坐标扩大为原来的 倍，得到曲线 ．
∴伸缩变换为 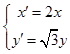，∴曲线 ： =1，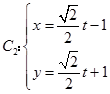
（t为参数）代入曲线 ，整理得 ．
∵t1t2＜0，（8分）
∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|=
【解析】（Ⅰ）求出曲线C1的直角坐标方程为：x2+y2=1，C2：y=x+2，再求出圆心到直线距离，由此能求出曲线C1上的点到曲线C2距离的最小值．（Ⅱ）伸缩变换为 ，从而曲线 ： =1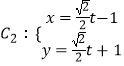， （t为参数）代入曲线 ，得 ．由此能求出|PA|+|PB|．