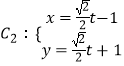题目内容
【题目】已知:在直角坐标系xOy中,曲线C的参数方程为:  为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系.求曲线C的极坐标方程.
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系.求曲线C的极坐标方程.
【答案】ρ=2cosθ(ρ>0)
【解析】试题分析:
消去参数![]() 可得曲线C的普通方程,从而知曲线是圆,且圆心为
可得曲线C的普通方程,从而知曲线是圆,且圆心为![]() ,半径为1,由此可得曲线C的极坐标方程,也可直直角坐标方程为用
,半径为1,由此可得曲线C的极坐标方程,也可直直角坐标方程为用![]() 代入得极坐标方程.
代入得极坐标方程.
试题解析:
∵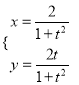 ,∴由t2≥0,可得0<x≤2,
,∴由t2≥0,可得0<x≤2,
将参数方程中的两式相除,可得得![]() ,
,
将![]() 代入
代入![]() ,化简可得x2+y2﹣2x=0(x>0)…①,
,化简可得x2+y2﹣2x=0(x>0)…①,
表示以(1,0)为圆心,半径r=1的圆.
又∵极坐标中x=ρcosθ,y=ρsinθ,
∴将(ρcosθ,ρsinθ)代入①,得ρ2cos2θ+ρ2sin2θ﹣2ρcosθ=0,
化简得ρ=2cosθ(ρ>0),即为曲线C的极坐标方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】汽车租赁公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表:
A型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(1)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(2)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(3)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.