题目内容
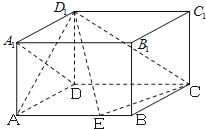
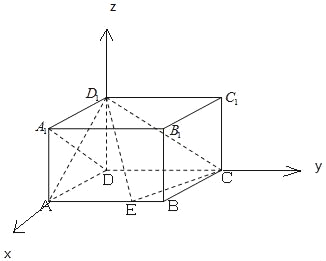
【题目】已知在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ)求证:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在点E使得AD1与平面D1EC成的角为![]() ?若存在,求出AE的长,若不存在,说明理由.
?若存在,求出AE的长,若不存在,说明理由.
【答案】(Ⅰ)证明见解析;(2)![]() .
.
【解析】试题分析:
(Ⅰ)要证![]() ,由正方形有
,由正方形有![]() ,因此要证
,因此要证![]() 平面
平面![]() ,而要证此线面垂直,只要证
,而要证此线面垂直,只要证![]() ,这由长方体的性质可得;(Ⅱ)假设存在,以D为原点,建立空间直角坐标系,写出各点坐标,并设
,这由长方体的性质可得;(Ⅱ)假设存在,以D为原点,建立空间直角坐标系,写出各点坐标,并设![]() ,用向量法求出AD1与平面D1EC成的角,从而求出
,用向量法求出AD1与平面D1EC成的角,从而求出![]() ,若能求出
,若能求出![]() ,说明存在,若不能求出
,说明存在,若不能求出![]() ,说明不存在.
,说明不存在.
试题解析:
(Ⅰ)证明:∵AE⊥平面AA1DD1,A1D平面AA1DD1,
∴AE⊥A1D,
∵在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,
∴A1D⊥AD1,
∵AE∩AD1=A,∴A1D⊥平面AED1,
∵D1E平面AED1,∴A1D⊥D1E.
(Ⅱ)解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设棱AB上存在点E(1,t,0),(0≤t≤2),使得AD1与平面D1EC成的角为![]() ,
,
A(1,0,0),D1(0,0,1),C(0,2,0),
![]() =(﹣1,0,1),
=(﹣1,0,1),![]() =(0,﹣2,1),
=(0,﹣2,1),![]() =(1,t﹣2,0),
=(1,t﹣2,0),
设平面D1EC的法向量为![]() =(x,y,z),
=(x,y,z),
则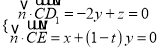 ,取y=1,得
,取y=1,得![]() =(t﹣1,1,2),
=(t﹣1,1,2),
∴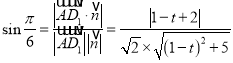 ,
,
整理,得t2﹣10t+12=0,
解得![]() 或
或![]() (舍),
(舍),
∴在棱AB上存在点E使得AD1与平面D1EC成的角为![]() ,AE=
,AE=![]() .
.

练习册系列答案
相关题目